题目内容
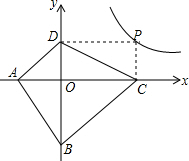
8.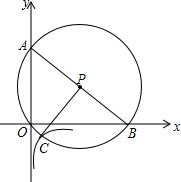 如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.
如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.
分析 连接AC,BC,过C作CE⊥x轴,CD⊥y轴,由CP垂直平分AB,得到CA=CB,利用同弧所对的圆周角相等得到一对角相等,再由一对直角相等,利用AAS得到三角形ADC与三角形BEC全等,利用全等三角形对应边相等得到AD=BE,CD=CE,得出C横纵坐标绝对值相等,设为(m,-m),由OB-OA=4,设OA=a,得出OB=a+4,由AD=BE求出m的值,确定出C坐标,代入反比例解析式求出k的值即可.
解答 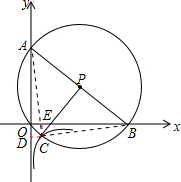 解:连接AC,BC,过C作CE⊥x轴,CD⊥y轴,
解:连接AC,BC,过C作CE⊥x轴,CD⊥y轴,
∵P为AB的中点,且CP⊥AB,即CP垂直平分AB,
∴AC=BC,
∵∠DAC与∠EBC都对$\widehat{OC}$,
∴∠DAC=∠EBC,
在△ADC和△BEC中,
$\left\{\begin{array}{l}{∠ADC=∠BEC=90°}\\{∠DAC=∠EBC}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△BEC(AAS),
∴CD=CE,AD=BE,
设C(m,-m),由OB-OA=4,设OA=a,则有OB=a+4,
∵AD=OA+OD=a+m,BE=OB-OE=a+4-m,
∴a+m=a+4-m,
解得:m=2,即C(2,-2),
把C坐标代入反比例解析式得:k=-4,
故答案为:-4
点评 此题属于反比例函数综合题,涉及的知识有:线段垂直平分线定理,全等三角形的判定与性质,坐标与图形性质,以及待定系数法确定反比例解析式,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
3.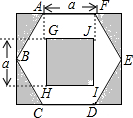 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )| A. | a2 | B. | ($\frac{\sqrt{3}}{2}$+1)a2 | C. | 2a2 | D. | $\frac{\sqrt{3}+1}{2}$a2 |
 阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.
阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.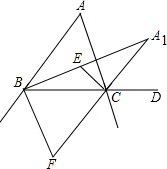 如图,在△ABC中,点E是∠ABC、∠ACB角平分线的交点,点F是∠ABC、∠ACB外角平分线的交点,点A1是内角∠ABC、外角∠ACD平分线的交点.
如图,在△ABC中,点E是∠ABC、∠ACB角平分线的交点,点F是∠ABC、∠ACB外角平分线的交点,点A1是内角∠ABC、外角∠ACD平分线的交点.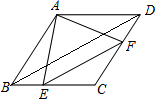 如图,在菱形ABCD中,∠ABC中,∠ABC=60°,点E、F分别从点B、D同时出发,以同样的速度沿边BC、DC向点C运动(点E、F不与点B、D重合).给出以下四个结论:①AE=AF;②EF∥BD;③当点E、F分别为边BC、DC的中点时,EF=$\sqrt{3}$BE;④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的个数有( )
如图,在菱形ABCD中,∠ABC中,∠ABC=60°,点E、F分别从点B、D同时出发,以同样的速度沿边BC、DC向点C运动(点E、F不与点B、D重合).给出以下四个结论:①AE=AF;②EF∥BD;③当点E、F分别为边BC、DC的中点时,EF=$\sqrt{3}$BE;④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的个数有( )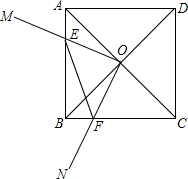 如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.
如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.