题目内容
13.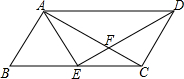 如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)
如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)①AD=2AB;②DF平分∠ADC;③S△ADE=2S△CDF;④AE⊥DE.
分析 由E是?ABCD的边BC的中点,AC⊥AB,根据直角三角形斜边的中线等于斜边的一半,可得AE=BE=CE=$\frac{1}{2}$BC,又由∠B=60°,可证得△ABE是等边三角形,即可证得AD=2AB;易求得∠CDA=∠B=60°,则可得DF平分∠ADC,由BE=CE,AD∥BC,可得S△ABE=S△DEC,然后由等高三角形的面积比等于对应底的比,求得S△ADE=$\frac{3}{2}$S△CDF;易得∠DAE=∠AEB=60°,∠ADE=30°,证得∠AED=90°.
解答 解:∵E是?ABCD的边BC的中点,AC⊥AB,
∴AE=BE=CE=$\frac{1}{2}$BC,
∵∠B=60°,
∴△ABE是等边三角形,
∴AB=BE,
∴BC=2AB;故①正确;
∵∠B=60°,
∴∠ECD=120°,
∵CE=CD,
∴∠CDE=30°,
∵∠CDA=∠B=60°,
∴DF平分∠ADC,故②正确;
∵BE=CE,AD∥BC,
∴S△ABE=S△DEC,
∵∠ACE=∠DEC=30°,
∴EF=CF,
∵AD∥BC,
∴△ADF∽△CEF,
∴CF:AF=EC:AD=1:2,
∴EF=CF=$\frac{1}{2}$AF,
∴S△CDF=$\frac{1}{2}$S△ADF,S△CDF=S△AEF,
∴S△ADE=$\frac{3}{2}$S△CDF;故③错误;
∵∠DAE=∠AEB=60°,∠ADE=30°,
∴∠AED=90°,
∴AE⊥DE,故④正确.
故答案为:①②④.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.注意相似三角形的对应边成比例以及等高三角形的面积比等于对应底的比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.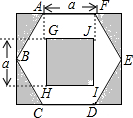 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )| A. | a2 | B. | ($\frac{\sqrt{3}}{2}$+1)a2 | C. | 2a2 | D. | $\frac{\sqrt{3}+1}{2}$a2 |
8.某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.(1)若今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,写出y与x的函数关系式;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为30;
②求在m天内日销售利润少于32元的天数;
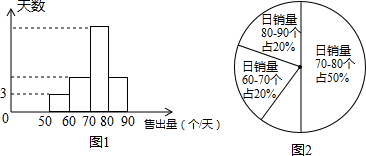
(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
请计算该组内平均每天销售面包的个数.
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分别直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图,如图1、图2所示,请结合两图提供的信息,解答下列问题:
①m的值为30;
②求在m天内日销售利润少于32元的天数;

(3)如图(2)中m天内日销售面包个数在70≤x<80这个组内的销售情况如表:
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
5.下列二次根式中,化简后不能与$\frac{1}{3}$$\sqrt{2}$进行加减运算的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | -$\sqrt{12}$ | D. | 6$\sqrt{18}$ |
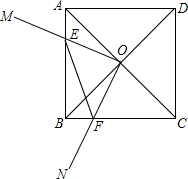 如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.
如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F. 已知:如图,∠ADC=∠CBA,∠1=∠2,求证:AD∥BC.
已知:如图,∠ADC=∠CBA,∠1=∠2,求证:AD∥BC.