题目内容
15.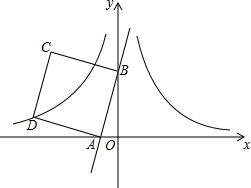 如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD.将过D点的双曲线y=$\frac{{k}_{1}}{x}$(x<0)沿y轴对折,得到双曲线y=$\frac{{k}_{2}}{x}$(x>0),将正方形ABCD沿x轴正方向向右平移a个单位长度后,点C恰好也落在此双曲线y=$\frac{{k}_{2}}{x}$(x>0)上,则a的值是( )
如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD.将过D点的双曲线y=$\frac{{k}_{1}}{x}$(x<0)沿y轴对折,得到双曲线y=$\frac{{k}_{2}}{x}$(x>0),将正方形ABCD沿x轴正方向向右平移a个单位长度后,点C恰好也落在此双曲线y=$\frac{{k}_{2}}{x}$(x>0)上,则a的值是( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
分析 作DE⊥x轴于E,作CF⊥y轴于F,先证明△ADE≌△BAO,得出DE=AO=1,AE=BO=3,同理可证△BCF≌△BAO,得出BF=AO=1,CF=BO=3,求出点D、点C的坐标,再求出双曲线的解析式,求出M的坐标,根据双曲线的对称性得出N的坐标,得出FN=FM,求出CN,即可得出a的值.
解答 解:作DE⊥x轴于E,作CF⊥y轴于F,交双曲线y=$\frac{{k}_{1}}{x}$(x<0)于M,交双曲线y=$\frac{{k}_{2}}{x}$(x>0)于N,如图所示: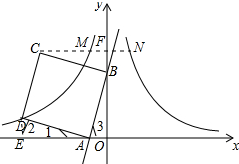 则∠DEA=∠CFB=90°,
则∠DEA=∠CFB=90°,
∴∠1+∠2=90°,
∵直线y=3x+3与x轴、y轴分别交于A、B两点,当y=0时,x=-1;
当x=0时,y=3,
∴AO=1,BO=3,
∵四边形ABCD是正方形,
∴AD=AB=BC,∠BAD=∠ABC=90°,
∴∠1+∠3=90°,
∴∠2=∠3,
在△ADE和△BAO中,$\left\{\begin{array}{l}{∠DEA=∠AOB=90°}&{\;}\\{∠2=∠3}&{\;}\\{AD=AB}&{\;}\end{array}\right.$,
∴△ADE≌△BAO(AAS),
同理:△BCF≌△BAO,
∴DE=AO=1,AE=BO=3,BF=AO=1,CF=BO=3,
∴OE=1+3=4,OF=1+3=4,
∴D的坐标为:(-4,1),C的坐标为:(-3,4),
把D(-4,1)代入y=$\frac{{k}_{1}}{x}$得:k1=-4,
∴y=-$\frac{4}{x}$,
当y=4时,x=-1,
∴M(-1,4),
∵双曲线y=$\frac{{k}_{1}}{x}$(x<0)和双曲线y=$\frac{{k}_{2}}{x}$(x>0)关于y轴对称,
∴N和M关于y轴对称,
∴N(1,4),
∴FN=FM=1,
∴a=CN=3+1=4;
故选:B.
点评 本题是反比例函数综合题目,考查了正方形的性质、全等三角形的判定与性质、反比例函数解析式的求法、对称的性质等知识;本题难度较大,综合性强,证明三角形全等和确定反比例函数解析式是解决问题的关键.

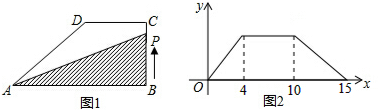
| A. | 18 | B. | 32 | C. | 48 | D. | 72 |
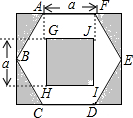 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )| A. | a2 | B. | ($\frac{\sqrt{3}}{2}$+1)a2 | C. | 2a2 | D. | $\frac{\sqrt{3}+1}{2}$a2 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
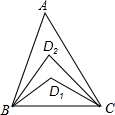 如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )| A. | 24° | B. | 25° | C. | 30° | D. | 36° |
| A. | $\sqrt{3}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | -$\sqrt{12}$ | D. | 6$\sqrt{18}$ |
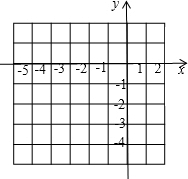 如图所示,已知△ABC是格点三角形
如图所示,已知△ABC是格点三角形