题目内容
10.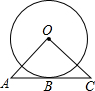 如图,AC经过⊙O上的一点B,AB=BC,连接OA、OC,∠A=∠C,求证:AB是⊙O的切线.
如图,AC经过⊙O上的一点B,AB=BC,连接OA、OC,∠A=∠C,求证:AB是⊙O的切线.
分析 连接OB,由等角对等边得出OA=OC,由等腰三角形的三线合一性质得出OB⊥AC,即可得出结论.
解答 证明:连接OB,如图所示:
∵∠A=∠C,
∴OA=OC,
∵AB=BC,
∴OB⊥AC,
∴AB是⊙O的切线.
点评 本题考查了切线的判定、等腰三角形的判定与性质;熟练掌握等腰三角形的三线合一性质,证出OB⊥AC是解决问题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
1. 一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
 一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )
一次函数y=kx+b的图象如图,则当0<x≤1时,y的范围是( )| A. | y>0 | B. | -2<y≤0 | C. | -2<y≤1 | D. | 无法判断 |
15.下列关于x的方程中,一定有实数根的是( )
| A. | $\sqrt{2x+3}$+4=0 | B. | $\sqrt{x-7}$+$\sqrt{x}$=7 | C. | $\sqrt{x-3}$=1-x | D. | $\sqrt{x-1}$+$\sqrt{1-x}$=3 |
19.下列运动属于数学上的旋转的有( )
| A. | 钟表上的时针运动 | B. | 城市环路公共汽车 | ||
| C. | 地球绕太阳转动 | D. | 将等腰三角形沿着底边上的高对折 |
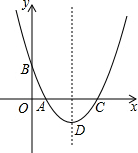 如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0).
如图,已知二次函数y=x2+bx+c的图象关于直线x=2对称,且与x轴交于A、C两点,与y轴交于点B,点C与坐标原点不重合,其坐标为(c,0).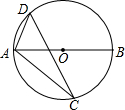 如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=48°.
如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=48°.