题目内容
1．
一次函数y=kx+b的图象如图，则当0＜x≤1时，y的范围是（ ）| A． | y＞0 | B． | -2＜y≤0 | C． | -2＜y≤1 | D． | 无法判断 |
分析 根据一次函数的图象与两坐标轴的交点直接解答即可．
解答 解：因为一次函数y=kx+b的图象与两坐标轴的交点分别为（1，0）、（0，-2），
所以当0＜x≤1，函数y的取值范围是：-2＜y≤0，
故选B
点评 本题考查的是用数形结合的方法求函数的取值范围，解答此题的关键是正确观察函数在平面直角坐标系内的图象，属较简单题目．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
实数a，b在数轴上的所对应的点的位置如图所示，化简$\sqrt{4{a^2}}-\sqrt{（a+b{）^2}}$=-3a-b．
如图，在正方形ABCD，E、F分别为DC、BC中点，求证：△ADE≌△ABF．
如图，△ABC中，∠B=90°，BC=2AB，则cosA=$\frac{\sqrt{5}}{5}$．
如图，有一个长为50cm，宽为30cm，高为40cm的长方体木箱，一根长70cm的木棍能放入（填“能”或“不能”）．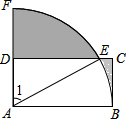
如图，在矩形ABCD中，AB=4，BC=2，以A为圆心，AB的长为半径画弧，交DC于点E，交AD延长线于点F，则图中阴影部分的面积为8-4$\sqrt{3}$+$\frac{4}{3}$π．
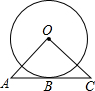如图，AC经过⊙O上的一点B，AB=BC，连接OA、OC，∠A=∠C，求证：AB是⊙O的切线．
11．计算：$\frac{\sqrt{3}+2\sqrt{5}+\sqrt{7}}{（\sqrt{3}+\sqrt{5}）（\sqrt{5}+\sqrt{7}）}$=（ ）
| A． | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | B． | $\frac{\sqrt{7}-\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}-\sqrt{7}}{2}$ | D． | $\frac{-\sqrt{7}-\sqrt{3}}{2}$ |