题目内容
20.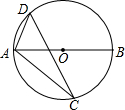 如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=48°.
如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=48°.
分析 先根据圆周角定理求出∠ACB=90°,再由三角形内角和定理得出∠ABC的度数,根据圆周角定理即可得出结论.
解答  解:如图,连接BC.
解:如图,连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=42°,
∴∠ABC=180°-90°-35°=48°,
∴∠ADC=∠ABC=48°.
故答案是:48°.
点评 本题考查的是圆周角定理,在解答此类问题时往往用到三角形的内角和是180°这一隐含条件.

练习册系列答案
相关题目
11.计算:$\frac{\sqrt{3}+2\sqrt{5}+\sqrt{7}}{(\sqrt{3}+\sqrt{5})(\sqrt{5}+\sqrt{7})}$=( )
| A. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | B. | $\frac{\sqrt{7}-\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-\sqrt{7}}{2}$ | D. | $\frac{-\sqrt{7}-\sqrt{3}}{2}$ |
15.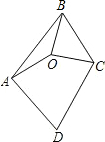 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )| A. | 70° | B. | 110° | C. | 140° | D. | 150° |
6.现有一只蜗牛和一只乌龟从同一点分别沿正东和正南方向爬行,蜗牛的速度为14厘米/分钟,乌龟的速度为48厘米/分钟,5分钟后,蜗牛和乌龟的直线距离为( )
| A. | 300厘米 | B. | 250厘米 | C. | 200厘米 | D. | 150厘米 |
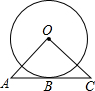 如图,AC经过⊙O上的一点B,AB=BC,连接OA、OC,∠A=∠C,求证:AB是⊙O的切线.
如图,AC经过⊙O上的一点B,AB=BC,连接OA、OC,∠A=∠C,求证:AB是⊙O的切线.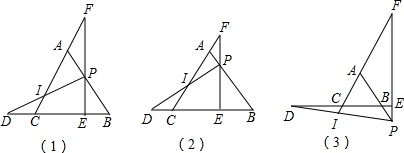
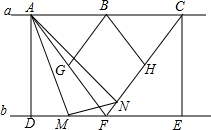 如图,直线a∥b,点A,B,C在直线a上,B是的AC中点,AC=4,分别过点A,C作直线b的垂线,垂足为D,E,F是直线b上的一个动点,连接AF,CF,若AF=CF.
如图,直线a∥b,点A,B,C在直线a上,B是的AC中点,AC=4,分别过点A,C作直线b的垂线,垂足为D,E,F是直线b上的一个动点,连接AF,CF,若AF=CF.