题目内容
17.在半径为2cm的⊙O中有一长度为2$\sqrt{3}$cm的弦,则该弦所对的圆周角度数等于60°或120°.分析 首先根据题意画出图形,过点O作OD⊥AB于点D,通过垂径定理,即可推出∠AOD的度数,求得∠AOB的度数,然后根据圆周角定理,即可推出∠AMB和∠ANB的度数.
解答 解:连接OA,过点O作OD⊥AB于点D,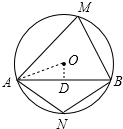
∵OA=2cm,AB=2$\sqrt{3}$cm,
∴AD=BD=2$\sqrt{3}$,
∴AD:OA=$\sqrt{3}$:2,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠AMB=60°,
∴∠ANB=120°.
故答案为:60°或120°.
点评 本题主要考查圆周角定理、垂径定理,关键在于根据题意正确的画出图形,运用圆周角定理和垂径定理认真的进行分析.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
2.在?ABCD中,∠D、∠C的度数之比为3:1,则∠A等于( )
| A. | 45° | B. | 135° | C. | 50° | D. | 130° |
9.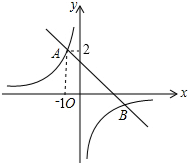 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,2),则另一个交点B的坐标为( )| A. | (-2,1) | B. | (2,1) | C. | (1,-2) | D. | (2,-1) |
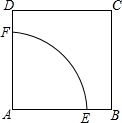 如图所示,公园里有一块边长为10米的正方形绿化地,现要在这块地上划出一个扇形区域举办花展,这个区域的面积是绿化地面积的一半,如图所示,正方形ABCD为绿化地,扇形EAF是所划区域,求AF的长(精确到0.1米).
如图所示,公园里有一块边长为10米的正方形绿化地,现要在这块地上划出一个扇形区域举办花展,这个区域的面积是绿化地面积的一半,如图所示,正方形ABCD为绿化地,扇形EAF是所划区域,求AF的长(精确到0.1米).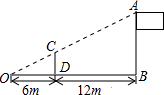 (1)如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为9m.
(1)如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为9m.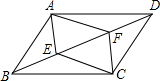 如图,在?ABCD中,E、F是对角线BD上两点,且BE=DF,连结AE、CE、AF、CF,四边形AECF是平行四边形吗?为什么?
如图,在?ABCD中,E、F是对角线BD上两点,且BE=DF,连结AE、CE、AF、CF,四边形AECF是平行四边形吗?为什么?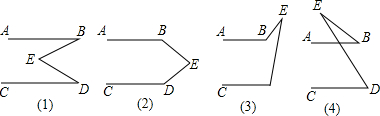
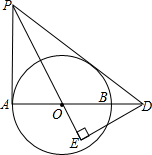 如图,在Rt△PAD中,∠PAD=90°,∠APD的角平分线PO交AD于O点,以O为圆心,OA为半径作⊙O,交AD于点B,过D作DE⊥PO交PO的延长线于点E.
如图,在Rt△PAD中,∠PAD=90°,∠APD的角平分线PO交AD于O点,以O为圆心,OA为半径作⊙O,交AD于点B,过D作DE⊥PO交PO的延长线于点E.