题目内容
函数y=2x和y=ax+4的图象相交于A(m,3),则方程组
的解为 .
|
考点:一次函数与二元一次方程(组)
专题:
分析:根据两函数图象的交点坐标满足方程组,方程组的解就是交点坐标.
解答:解:∵函数y=2x和y=ax+4的图象相交于A(m,3),
∴3=2m,
解得m=1.5,
则方程组
的解为
.
故答案为
.
∴3=2m,
解得m=1.5,
则方程组
|
|
故答案为
|
点评:本题主要考查了函数解析式与图象的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
如图所示图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第(20)个图形中圆的个数为( )


| A、781 | B、784 |
| C、787 | D、678 |
已知-1≤a≤1,则x2+(a-4)x+4-2a>0的解为( )
| A、x>3或x<2 |
| B、x>2或x<1 |
| C、x>3或x<1 |
| D、1<x<3 |
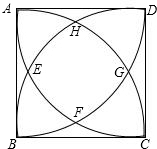 如图,这是当初中央电视台设计台徽时的模型,它是以正方形ABCD的每个顶点为圆心,每边长为半径画圆弧交于E、F、G、H.若边长AB=4cm,则点F到BC的距离是
如图,这是当初中央电视台设计台徽时的模型,它是以正方形ABCD的每个顶点为圆心,每边长为半径画圆弧交于E、F、G、H.若边长AB=4cm,则点F到BC的距离是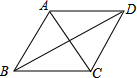 如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠BDC的度数为
如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠BDC的度数为