题目内容
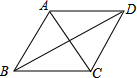 如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠BDC的度数为
如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠BDC的度数为考点:角平分线的性质
专题:
分析:延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,根据BD是∠ABC的平分线可得出△BDE≌△BDF,故DE=DF,过D点作DG⊥AC于G点,可得出△ADE≌△ADG,△CDG≌△CDF,进而得出CD为∠ACF的平分线,得出∠DCA=54°,再根据∠ADC=180°-∠DAC-∠DCA即可得出结论.
解答:解:延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,
∵BD是∠ABC的平分线
在△BDE与△BDF中,
,
∴△BDE≌△BDF(ASA),
∴DE=DF,
又∵∠BAD+∠CAD=180°
∠BAD+∠EAD=180°
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
过D点作DG⊥AC于G点,
在Rt△ADE与Rt△ADG中,
,
∴△ADE≌△ADG(HL),
∴DE=DG,
∴DG=DF.
在Rt△CDG与Rt△CDF中,
,
∴Rt△CDG≌Rt△CDF(HL)
∴CD为∠ACF的平分线
∠ACB=72°
∴∠DCA=54°,
△ABC中,
∵∠ACB=72°,∠ABC=50°,
∴∠BAC=180°-72°-50°=58°,
∴∠DAC=
=61°,
∴∠ADC=180°-∠DAC-∠DCA=180°-61°-54°=65°,
∴∠BDC=180°-25°-54°-72°=29°.
故答案为:29°.
∵BD是∠ABC的平分线
在△BDE与△BDF中,

|
∴△BDE≌△BDF(ASA),
∴DE=DF,
又∵∠BAD+∠CAD=180°
∠BAD+∠EAD=180°
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
过D点作DG⊥AC于G点,
在Rt△ADE与Rt△ADG中,
|
∴△ADE≌△ADG(HL),
∴DE=DG,
∴DG=DF.
在Rt△CDG与Rt△CDF中,
|
∴Rt△CDG≌Rt△CDF(HL)
∴CD为∠ACF的平分线
∠ACB=72°
∴∠DCA=54°,
△ABC中,
∵∠ACB=72°,∠ABC=50°,
∴∠BAC=180°-72°-50°=58°,
∴∠DAC=
| 180°-58° |
| 2 |
∴∠ADC=180°-∠DAC-∠DCA=180°-61°-54°=65°,
∴∠BDC=180°-25°-54°-72°=29°.
故答案为:29°.
点评:本题考查了角平分想的性质,以及三角形的全等和三角形的内角和定理,注意知识点的综合运用.

练习册系列答案
相关题目
 如图,是一块电脑主板的示意图,每一转角处都是直角,数据如图(单位:mm),则该主板的周长是( )
如图,是一块电脑主板的示意图,每一转角处都是直角,数据如图(单位:mm),则该主板的周长是( )| A、88mm | B、96mm |
| C、80mm | D、84mm |
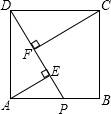 如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=3,CF=5,则EF=
如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=3,CF=5,则EF= 如图,?ABCD的周长是36cm,AB=8cm,BC=
如图,?ABCD的周长是36cm,AB=8cm,BC= ?ABCD中,DE平分∠ADC,交AB于E,AD=7,BE=2,则?ABCD的周长为
?ABCD中,DE平分∠ADC,交AB于E,AD=7,BE=2,则?ABCD的周长为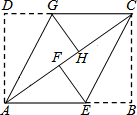 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC,AD恰好落在AC上,其中F,H分别是B,D的落点.求证:四边形AECG是平行四边形.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC,AD恰好落在AC上,其中F,H分别是B,D的落点.求证:四边形AECG是平行四边形.