题目内容
将3个相同的黑球和3个相同的白球自左向右排成一排,如果满足:从任何一个位置(含这个位置)开始向左数,黑球的个数不小于白球的个数,就称这种排列为“有效排列”,则出现“有效排列”的概率为 .
考点:列表法与树状图法
专题:
分析:由题意可求得所有等可能的结果与构成“有效排列”的有:黑黑黑白白,黑白黑白黑白,黑白黑黑白白,黑黑白黑白白,黑黑白白黑白,共五种,然后利用概率公式求解即可求得答案.
解答:解:∵由3个相同的黑球和3个相同的白球组成,自左向右排成一排全部的排法有:
=20(种),
构成“有效排列”的有:黑黑黑白白,黑白黑白黑白,黑白黑黑白白,黑黑白黑白白,黑黑白白黑白,共五种,
∴出现“有效排列”的概率为:
=
.
故答案为:
.
| 6×5×4×3×2×1 |
| (3×2×1)×(3×2×1) |
构成“有效排列”的有:黑黑黑白白,黑白黑白黑白,黑白黑黑白白,黑黑白黑白白,黑黑白白黑白,共五种,
∴出现“有效排列”的概率为:
| 5 |
| 20 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
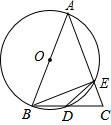 已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.(1)求∠EBC的度数;
(2)求证:BD=DC;
(3)若圆O的半径为
| 2 |
 |
| BD |
已知24+n•42n+1=(
)-n,则n为( )
| 1 |
| 8 |
| A、n=-3 | B、n=-2 |
| C、n=-1 | D、n=0 |
 如图,?ABCD的周长是36cm,AB=8cm,BC=
如图,?ABCD的周长是36cm,AB=8cm,BC= ?ABCD中,DE平分∠ADC,交AB于E,AD=7,BE=2,则?ABCD的周长为
?ABCD中,DE平分∠ADC,交AB于E,AD=7,BE=2,则?ABCD的周长为