题目内容
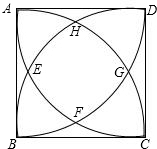 如图,这是当初中央电视台设计台徽时的模型,它是以正方形ABCD的每个顶点为圆心,每边长为半径画圆弧交于E、F、G、H.若边长AB=4cm,则点F到BC的距离是
如图,这是当初中央电视台设计台徽时的模型,它是以正方形ABCD的每个顶点为圆心,每边长为半径画圆弧交于E、F、G、H.若边长AB=4cm,则点F到BC的距离是考点:正方形的性质,等边三角形的性质,弧长的计算
专题:
分析:连接AF、DF,根据圆的定义判断出△ADF是等边三角形,根据等边三角形的性质求出点F到AD的距离,再求出点F到BC的距离即可;根据正方形和等边三角形的性质求出∠BAF=30°,同理可得弧DG的圆心角是30°,然后求出弧FG的圆心角是30°,再根据弧长公式求出弧FG的长,然后根据对称性,曲四边形的四条边都相等列式计算即可得解.
解答:解:如图,连接AF、DF,
由圆的定义,AD=AF=DF,
所以,△ADF是等边三角形,
所以,点F到AD的距离=
×4=2
,
所以,点F到BC的距离=(4-2
)cm;
∵∠BAD=90°,∠FAD=60°,
∴∠BAF=90°-60°=30°,
同理,弧DG的圆心角是30°,
∴弧FG的圆心角是90°-30°×2=30°,
∴
=
=
π,
由对称性知,曲四边形的四条边都相等,
所以,曲边四边形EFGH的周长=
π×4=
πcm.
故答案为:(4-2
)cm;
πcm.
由圆的定义,AD=AF=DF,
所以,△ADF是等边三角形,

所以,点F到AD的距离=
| ||
| 2 |
| 3 |
所以,点F到BC的距离=(4-2
| 3 |
∵∠BAD=90°,∠FAD=60°,
∴∠BAF=90°-60°=30°,
同理,弧DG的圆心角是30°,
∴弧FG的圆心角是90°-30°×2=30°,
∴
 |
| FG |
| 30•π•4 |
| 180 |
| 2 |
| 3 |
由对称性知,曲四边形的四条边都相等,
所以,曲边四边形EFGH的周长=
| 2 |
| 3 |
| 8 |
| 3 |
故答案为:(4-2
| 3 |
| 8 |
| 3 |
点评:本题考查了正方形的性质,等边三角形的判定,弧长的计算,作辅助线构造成等边三角形是解题的关键,难点在于熟练掌握图形的对称性.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 如图,是一块电脑主板的示意图,每一转角处都是直角,数据如图(单位:mm),则该主板的周长是( )
如图,是一块电脑主板的示意图,每一转角处都是直角,数据如图(单位:mm),则该主板的周长是( )| A、88mm | B、96mm |
| C、80mm | D、84mm |
 如图,在△ABC中,D、E分别是AB、AC的中点,延长DE到点F,使EF=DE,连接CF.
如图,在△ABC中,D、E分别是AB、AC的中点,延长DE到点F,使EF=DE,连接CF.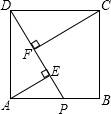 如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=3,CF=5,则EF=
如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=3,CF=5,则EF= 如图,?ABCD的周长是36cm,AB=8cm,BC=
如图,?ABCD的周长是36cm,AB=8cm,BC=