题目内容
16.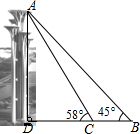 奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
分析 根据已知条件求出BD=AD,设DC=x,得出AD=90+x,再根据tan58°=$\frac{AD}{DC}$,求出x的值,即可得出AD的值.
解答 解:∵∠B=45°,AD⊥DB,
∴∠DAB=45°,
∴BD=AD,
设DC=x,则BD=BC+DC=90+x,
∴AD=90+x,
∴tan58°=$\frac{AD}{DC}$=$\frac{90+x}{x}$=1.60,
解得:x=150,
∴AD=90+150=240(米),
答:最高塔的高度AD约为240米.
点评 本题考查了解直角三角形的应用,要求学生能借助仰角构造直角三角形并解直角三角形,注意方程思想的运用.

练习册系列答案
相关题目
7. 如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
 如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )| A. | 2$\sqrt{3}$cm | B. | 3cm | C. | 4cm | D. | 2$\sqrt{5}$cm |
1.抛物线y=$\frac{1}{2}$x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为( )
| A. | y=$\frac{1}{2}$x2+2x+1 | B. | y=$\frac{1}{2}$x2+2x-2 | C. | y=$\frac{1}{2}$x2-2x-1 | D. | y=$\frac{1}{2}$x2-2x+1 |
6.在Rt△ABC中,CD是斜边AB上的高,∠A=30°,那么下列结论正确的是( )
| A. | 3AD=7BC | B. | AB=2AC | C. | AC=8CD | D. | 16CD2=3AB2 |
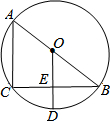 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC. 如图,⊙O的半径为5,AB为弦,OC⊥AB,交AB于点D,交⊙O于点C,CD=2,求弦AB的长.
如图,⊙O的半径为5,AB为弦,OC⊥AB,交AB于点D,交⊙O于点C,CD=2,求弦AB的长.