题目内容
11.二次函数y=2x2-8x+m满足以下条件:当-2<x<-1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,则m的值为( )| A. | 8 | B. | -10 | C. | -42 | D. | -24 |
分析 根据抛物线顶点式得到对称轴为直线x=2,通过顶点坐标位置特征求出m的范围,将A选项剔除后,将B、C、D选项带入其中,并根据二次函数对称性和增减性特点判断是否合理.
解答 不如先通过顶点坐标位置特征求出m的范围,将A选项剔除后,将B、C、D选项带入其中,并根据二次函数对称周两侧图象增减性特点令x=-2时y值小于零和x=6时y值大于零去取舍各位合理.忘菁优网老师能够采纳.
解:∵抛物线y=2x2-8x+m=2(x-2)2-8+m的对称轴为直线x=2,
而抛物线在-2<x<-1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方,
∴m<0,
当m=-10时,则y=2x2-8x-10,
令y=0,则2x2-8x-10=0,
解得x1=-1,x2=5,
则有当-2<x<-1时,它的图象位于x轴的上方;
当m=-42时,则y=2x2-8x-42,
令y=0,则2x2-8x-42=0,
解得x1=-3,x2=7,
则有当6<x<7时,它的图象位于x轴的下方;
当m=-24时,则y=2x2-8x-24,
令y=0,则2x2-8x-24=0,
解得x1=-2,x2=6,
则有当-2<x<-1时,它的图象位于x轴的下方;当6<x<7时,它的图象位于x轴的上方;
故选D.
点评 本题考查了抛物线与x轴的交点以及抛物线的轴对称性:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
6.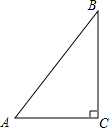 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
 实数a,b,c在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$+|a+b|-$\sqrt{{c}^{2}}$-|b-c|=0.
实数a,b,c在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$+|a+b|-$\sqrt{{c}^{2}}$-|b-c|=0. 如图,△ABC中,AB=AC,BD⊥AC,BD=6,E为AB边的中点,ED=5,则DC=2.
如图,△ABC中,AB=AC,BD⊥AC,BD=6,E为AB边的中点,ED=5,则DC=2.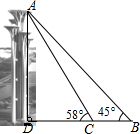 奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)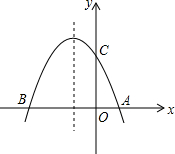 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.