题目内容
6.在Rt△ABC中,CD是斜边AB上的高,∠A=30°,那么下列结论正确的是( )| A. | 3AD=7BC | B. | AB=2AC | C. | AC=8CD | D. | 16CD2=3AB2 |
分析 根据∠A=30°,推知∠BCD=30°,在直角三角形CDB和ABC中,解直角三角形求得AD与CD、AB与AC、AC与CD的关系,再进一步推理即可.
解答  解:∵在Rt△ABC中,CD是斜边AB上的高,∠A=30°,
解:∵在Rt△ABC中,CD是斜边AB上的高,∠A=30°,
∴AD=$\sqrt{3}$CD,CD=$\frac{\sqrt{3}}{2}$BC,AC=$\frac{\sqrt{3}}{2}$AB,AC=2CD,CD=$\frac{\sqrt{3}}{2}$BC,BC=$\frac{1}{2}$AB,
∴AD=$\frac{3}{2}$BC,AB=$\frac{2\sqrt{3}}{3}$AC,CD=$\frac{\sqrt{3}}{2}$×$\frac{1}{2}$AB=$\frac{\sqrt{3}}{4}$AB,
∴4CD=$\sqrt{3}$AB,
∴16CD2=3AB2.
故选D.
点评 本题考查了含30°角的直角三角形,“30°的角所对的直角边是斜边的一半”是解题的关键.

练习册系列答案
相关题目
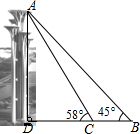 奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)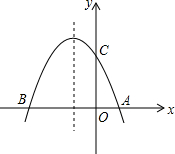 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1.
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于C点,且A(1,0),C(0,3),抛物线的对称轴为x=-1. 如图所示,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,∠ADB=100°,则∠BAC的度数是50°.
如图所示,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,∠ADB=100°,则∠BAC的度数是50°. 如图所示是长方体的表面展开图,折叠成一个长方体.
如图所示是长方体的表面展开图,折叠成一个长方体.