题目内容
1.有A、B两种饮料,这两种饮料的体积和单价如表:| 类型 | A | B |
| 单瓶饮料体积/升 | 1 | 2.5 |
| 单价/元 | 3 | 4 |
(2)若购买A、B两种饮料共36瓶,且A种饮料的数量不多于B种饮料的数量,则最少可以购买多少升饮料?
分析 (1)设他购买了A种饮料a瓶,B种饮料b瓶,根据“购买A、B两种饮料共13升;用了25元”列方程组求解即可;
(2)设购买了A种饮料x瓶,购买了y升饮料,首先确定自变量的取值范围,然后得到有关饮料总升和饮料瓶数之间的关系得到函数解析式,确定函数的最值即可.
解答 解:设他购买了A种饮料a瓶,B种饮料b瓶.
则由题意可得$\left\{\begin{array}{l}{a+2.5b=13}\\{3a+4b=25}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=3}\\{b=4}\end{array}\right.$.
故他购买了3瓶A种饮料,4瓶B种饮料;
(2)设购买了A种饮料x瓶,购买了y升饮料,
则x≥0且x≤36-x,解得0≤x≤18,
由题意可得y=x+2.5(36-x)--1.5x+90,
∵-1.5<0,
∴y随的增大而减小,
当x=18时,ymin=-1.5×18+90=63.
∴最少可以购买63升饮料.
点评 此题主要考查了二元一次方程组的应用以及一次函数的应用等知识,根据题意得出正确的等量关系是解题关键,难度不大.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
11.已知关于x、y的二元一次方程组$\left\{\begin{array}{l}{x+y=5}\\{x-y=9}\end{array}\right.$,则代数式2x+y的值( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
9.以下列各组数据为边不能组成直角三角形的一组数据是( )
| A. | 3,4,5 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 6,8,10 | D. | 5,12,13 |
 如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠ACB的值为$\frac{\sqrt{5}}{5}$.
如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠ACB的值为$\frac{\sqrt{5}}{5}$. 如图,AD是Rt△ABC斜边上的高.若AB=4cm,BC=10cm,则BD=1.6cm.
如图,AD是Rt△ABC斜边上的高.若AB=4cm,BC=10cm,则BD=1.6cm. 如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
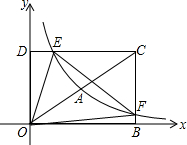 如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系中,已知四边形DOBC是矩形,且D(0,2),B(3,0).若反比例函数y=-$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F,设直线EF的解析式为y=k2x+b.