题目内容
6. 如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.
如图,在?ABCD中,过点A作AE⊥BC于点E,AF⊥DC于点F,AE=AF.(1)求证:四边形ABCD是菱形;
(2)若∠EAF=60°,CF=2,求AF的长.
分析 (1)方法一:连接AC,利用角平分线判定定理,证明DA=DC即可;方法二:只要证明△AEB≌△AFD.可得AB=AD即可解决问题.
(2)在Rt△ACF,根据AF=CF•tan∠ACF计算即可.
解答 (1)证法一:连接AC,如图.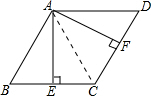
∵AE⊥BC,AF⊥DC,AE=AF,
∴∠ACF=∠ACE,
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAC=∠ACB.
∴∠DAC=∠DCA,
∴DA=DC,
∴四边形ABCD是菱形.
证法二:如图,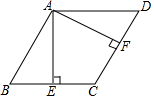
∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥DC,
∴∠AEB=∠AFD=90°,
又∵AE=AF,
∴△AEB≌△AFD.
∴AB=AD,
∴四边形ABCD是菱形.
(2)解:连接AC,如图.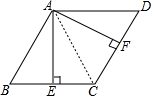
∵AE⊥BC,AF⊥DC,∠EAF=60°,
∴∠ECF=120°,
∵四边形ABVD是菱形,
∴∠ACF=60°,
在Rt△CFA中,AF=CF•tan∠ACF=2$\sqrt{3}$.
点评 本题考查菱形的性质和判定、平行四边形的性质、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.有A、B两种饮料,这两种饮料的体积和单价如表:
(1)小明购买A、B两种饮料共13升,用了25元,他购买A,B两种饮料个各多少瓶?
(2)若购买A、B两种饮料共36瓶,且A种饮料的数量不多于B种饮料的数量,则最少可以购买多少升饮料?
| 类型 | A | B |
| 单瓶饮料体积/升 | 1 | 2.5 |
| 单价/元 | 3 | 4 |
(2)若购买A、B两种饮料共36瓶,且A种饮料的数量不多于B种饮料的数量,则最少可以购买多少升饮料?
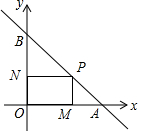 如图,P点的坐标为(3,2),过P点的直线AB分别交x轴和y轴的正半轴于A,B两点,作PM⊥x轴于M点,作PN⊥y轴于N点,若△PAM的面积与△PBN的面积的比为$\frac{4}{9}$,则直线AB的解析式为y=-x+5.
如图,P点的坐标为(3,2),过P点的直线AB分别交x轴和y轴的正半轴于A,B两点,作PM⊥x轴于M点,作PN⊥y轴于N点,若△PAM的面积与△PBN的面积的比为$\frac{4}{9}$,则直线AB的解析式为y=-x+5.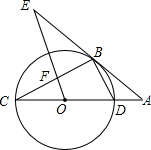 如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,∠AEO=∠C,OE交BC于点F.
如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,∠AEO=∠C,OE交BC于点F.