题目内容
从-4,-2,0,2,4这5个数中任取一个数,作为关于x的一元二次方程x2-2x-k=0的k值,则所得的方程中有两个不相等的实数根的概率是 .
考点:根的判别式,概率公式
专题:计算题
分析:先根据判别式的意义得到△=(-2)2-4×(-k)>0,解得 k>-1,再判断所给5个数中0,2,4满足条件,然后根据概率公式求解.
解答:解:根据题意得△=(-2)2-4×(-k)>0,
解得 k>-1,
所以-4,-2,0,2,4这5个数中有0,2,4满足 k>-1,
所以所得的方程中有两个不相等的实数根的概率是
.
故答案为
.
解得 k>-1,
所以-4,-2,0,2,4这5个数中有0,2,4满足 k>-1,
所以所得的方程中有两个不相等的实数根的概率是
| 3 |
| 5 |
故答案为
| 3 |
| 5 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了概率公式.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
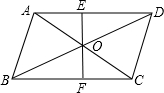 如图,在?ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC边分别交于点E,F.如果AB=4,BC=5,OE=1.5,求四边形CDEF的周长.
如图,在?ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC边分别交于点E,F.如果AB=4,BC=5,OE=1.5,求四边形CDEF的周长. 把一副直角三角尺按如图所示叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°,则这副直角三角尺重叠部分的面积为
把一副直角三角尺按如图所示叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°,则这副直角三角尺重叠部分的面积为 如图,已知AD是等腰△ABC底边上的高,且tanB=
如图,已知AD是等腰△ABC底边上的高,且tanB= 如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是
如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是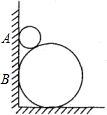 如图,两圆轮叠靠在墙边,如果大圆轮半径R为90cm,AB=60cm,则小圆轮半径r为
如图,两圆轮叠靠在墙边,如果大圆轮半径R为90cm,AB=60cm,则小圆轮半径r为