题目内容
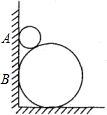如图，两圆轮叠靠在墙边，如果大圆轮半径R为90cm，AB=60cm，则小圆轮半径r为考点：相切两圆的性质
专题：
分析：根据相切两圆的性质得出得出在Rt△NEM中，NE2+ME2=MN2，进而求出r的值即可．
解答：
解：如图所示：设两圆心分别为N，M，连接MN，AN，BM，过点N作NE⊥BM于点M，
∵大圆轮半径R为90cm，AB=60cm，
∴ME=60cm，ME=90-AN，
∴在Rt△NEM中，
NE2+ME2=MN2，
∴602+（90-r）2=（90+r）2，
解得：r=10，
故答案为：10．
解：如图所示：设两圆心分别为N，M，连接MN，AN，BM，过点N作NE⊥BM于点M，∵大圆轮半径R为90cm，AB=60cm，
∴ME=60cm，ME=90-AN，
∴在Rt△NEM中，
NE2+ME2=MN2，
∴602+（90-r）2=（90+r）2，
解得：r=10，
故答案为：10．
点评：此题主要考查了相切两圆的性质以及勾股定理等知识，利用已知构造直角三角形是解题关键．
练习册系列答案
相关题目
如图，用20m的篱笆围成一个矩形的花圃．设连墙的一边为x（m），矩形的面积为y（m2）．
如图△ABE沿BC方向平移到△FCD的位置，若有AB=4，AE=3，BC=5，则CF=
如图①，一个圆球放置在V形架中，图②是它的平面示意图，CA和CB都是⊙O的切线，切点分别是A，B．如果⊙O的半径为2
如图，现测量河宽AB（假设河的两岸平行），在点C测得∠ACB=30°，在点D测得∠ADB=45°．若CD=60m，则河宽AB为