题目内容
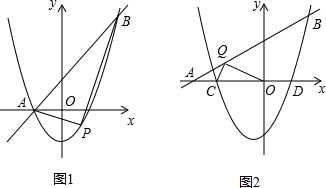
11.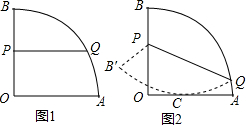 如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.
如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.(1)当P是OB中点,且PQ∥OA时(如图1),弧AQ的长为$\frac{2}{3}$π;
(2)将扇形OAB沿PQ对折,使折叠后的弧QB′恰好与半径OA相切于C点(如图2).若OP=3,则O到折痕PQ的距离为$\sqrt{6}$.
分析 (1)要想求弧长,就得求$\widehat{AD}$所对的圆心角的度数,所以要连接OQ,构成圆心角,利用直角三角形直角边是斜边的一半,则这条直角边所对的锐角为30°求出∠1=30°,再利用平行线截得内错角相等得出∠2的度数,代入弧长公式计算即可.
(2)先找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,证明四边形OCO′B是矩形,由勾股定理求O′B,从而求出OO′的长,则OM=$\frac{1}{2}$OO′=$\sqrt{6}$.
解答 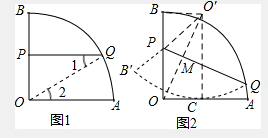 解:(1)如图1,连接OQ,
解:(1)如图1,连接OQ,
∵扇形OAB的半径为4且P是OB中点,
∴OP=2,OQ=4,
∵PQ∥OA,
∴∠BPQ=∠AOB=90°,
∴∠1=30°,
∴∠2=∠1=30°,
由弧AQ的长=$\frac{30×π×4}{180}$=$\frac{2}{3}$π,
故答案为:$\frac{2}{3}$π;
(2)如图2,找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,
则OM=O′M,OO′⊥PQ,O′P=OP=3,点O′是$\widehat{B′Q}$所在圆的圆心,
∴O′C=OB=4,
∵折叠后的弧QB′恰好与半径OA相切于C点,
∴O′C⊥AO,
∴O′C∥OB,
∴四边形OCO′B是矩形,
在Rt△O′BP中,O′B=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
在Rt△OBO′K,OO′=$\sqrt{{4}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$,
∴OM=$\frac{1}{2}$OO′=$\frac{1}{2}$×2$\sqrt{6}$=$\sqrt{6}$,
即O到折痕PQ的距离为$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题考查了折叠问题和圆的切线的性质、矩形的性质和判定,熟练掌握弧长公式l=$\frac{nπR}{180}$(n为圆心角度数,R为圆半径),明确过圆的切线垂直于过切点的半径,这是常考的性质;对称点的连线被对称轴垂直平分.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 奖项 | 一等奖 | 二等奖 | 三等奖 |
| |x| | |x|=4 | |x|=3 | 1≤|x|<3 |
(2)是否每次抽奖都会获奖,为什么?
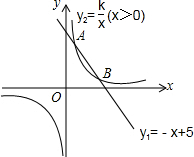 如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).
如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n). 将抛物线c1:$y=-\sqrt{3}{x^2}+\sqrt{3}$沿x轴翻折,得到抛物线c2,如图1所示.
将抛物线c1:$y=-\sqrt{3}{x^2}+\sqrt{3}$沿x轴翻折,得到抛物线c2,如图1所示.
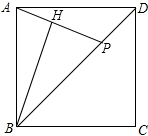 已知正方形ABCD的边长是2,点P从点D出发沿DB向点B运动,至点B停止运动,连结AP,过点B作BH⊥AP于点H,在点P运动过程中,点H所走过的路径长是π.
已知正方形ABCD的边长是2,点P从点D出发沿DB向点B运动,至点B停止运动,连结AP,过点B作BH⊥AP于点H,在点P运动过程中,点H所走过的路径长是π. 如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8cm.
如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8cm.