题目内容
1.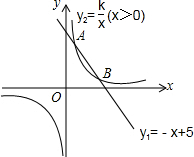 如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).
如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于点A(m,4)和点B(4,n).(1)求m,n的值和反比例函数的表达式;
(2)根据图象,直接写出函数值y2>y1对应的自变量x的取值范围.
分析 (1)根据点A(m,4)和点B(4,n)都在一次函数y1=-x+5的图象上即可求出m和n的值,进而求出反比例函数系数k的值;
(2)根据图形即可求出函数值y2>y1对应的自变量x的取值范围.
解答 解:(1)∵点A(m,4)和点B(4,n)都在一次函数y1=-x+5的图象上,
∴$\left\{\begin{array}{l}{-m+5=4}\\{-4+5=n}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=1}\\{n=1}\end{array}\right.$,
∴点A坐标为(1,4),点B坐标为(4,1),
又∵点A(1,4)在反比例函数y2=$\frac{k}{x}$(x>0)的图象上,
∴k=4,
∴反比例函数的解析式为y2=$\frac{4}{x}$(x>0);
(2)函数值y2>y1对应的自变量x的取值范围是0<x<1或x>4.
点评 本题主要考查了反比例函数与一次函数的交点问题,解题的关键是求出m和n的值,此题难度不大.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
11.用总长为60cm的篱笆围成矩形场地.
(Ⅰ)根据题意,填写下表:
(Ⅱ)设矩形一边长为lm,矩形面积为Sm2,当l是多少时,矩形场地的面积S最大?并求出矩形场地的最大面积;
(Ⅱ)当矩形的长为18m,宽为12m时,矩形场地的面积为216m2.
(Ⅰ)根据题意,填写下表:
| 矩形一边长/m | 5 | 10 | 15 | 20 |
| 矩形面积/m2 | 125 | 200 | 225 | 200 |
(Ⅱ)当矩形的长为18m,宽为12m时,矩形场地的面积为216m2.

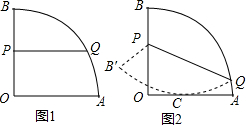 如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.
如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.