题目内容
16.用一段长32m的篱笆和长8m的墙,围成一个矩形的菜园.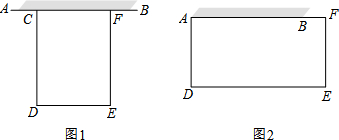
(1)如图1,如果矩形菜园的一边靠墙AB,另三边由篱笆CDEF围成.
①设DE等于x m,直接写出菜园面积y与x之间的函数关系式,并写出自变量的取值范围.
②菜园的面积能不能等于110m2?若能,求出此时x的值;若不能,请说明理由.
(2)如图2,如果矩形菜园的一边由墙AB和一节篱笆BF构成,另三边由篱笆ADEF围成,求菜园面积的最大值.
分析 (1)①首先设DE=xm,根据周长表示出CD=16-$\frac{1}{2}$x(m),进而利用矩形面积公式得出答案;
②利用一元二次方程的解法结合①中自变量取值范围得出答案;
(2)首先设BF=tm,则DE=(t+8)m、AD=(12-t)m,再利用矩形面积公式求出答案.
解答 解:(1)①设DE=xm,则CD=EF=16-$\frac{1}{2}$x(m),
则y=x(16-$\frac{1}{2}$x)=-$\frac{1}{2}$x2+16x,(0<x≤8);
②令y=110,即-$\frac{1}{2}$x2+16x=110,
解得:x1=10,x2=22,
∵0<x≤8,
∴x1=10,x2=22均不符合题意,
故菜园的面积不能等于110m2;
(2)设菜园的面积为S,BF=t(m),则DE=t+8(m),AD=EF=$\frac{32-t-(t+8)}{2}$=12-t(m),
则S=(t+8)(12-t)=-t2+4t+96=-(t-2)2+100,
∴当t=2时,S最大,最大值为100,
答:菜园面积的最大值为100m2.
点评 此题主要考查了二次函数的应用,根据题意正确表示出矩形的边长是解题关键.

练习册系列答案
相关题目
1.某市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A,B,C,D,E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.

调查测试成绩分组表
请你根据图中提供的信息解答以下问题:
(1)参加调查测试的学生为400人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩的中位数落在C组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2 600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.

调查测试成绩分组表
| A组:90≤x≤100 |
| B组:80≤x<90 |
| C组:70≤x<80 |
| D组:60≤x<70 |
| E组:x<60 |
(1)参加调查测试的学生为400人;
(2)将条形统计图补充完整;
(3)本次调查测试成绩的中位数落在C组内;
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2 600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.

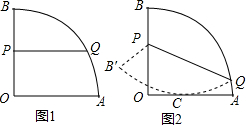 如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.
如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.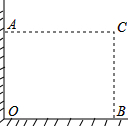 在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2. 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).