题目内容
1. 如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8cm.
如图,两同心圆的大圆半径长为5cm,小圆半径长为3cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8cm.
分析 根据切线的性质以及垂径定理,在Rt△BOC中利用勾股定理求出BC,即可得出AB的长.
解答 解:∵AB是⊙O切线,
∴OC⊥AB,
∴AC=BC,
在Rt△BOC中,∵∠BCO=90°,OB=5,OC=3,
∴BC=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm),
∴AB=2BC=8cm.
故答案为:8cm.
点评 本题考查切线的性质、垂径定理.勾股定理等知识,解题的关键是熟练运用这些知识解决问题,属于基础题中考常考题型.

练习册系列答案
相关题目
16.$\frac{1}{2016}$的倒数是( )
| A. | -$\frac{1}{2016}$ | B. | $\frac{1}{2016}$ | C. | 2016 | D. | -2016 |
13.某公司内设四个部门,2015年各部门人数及相应的每人所创年利润如表所示,求该公司2015年平均每人所创年利润.
| 部门 | 人数 | 每人所创年利润/万元 |
| A | 1 | 36 |
| B | 6 | 27 |
| C | 8 | 16 |
| D | 11 | 20 |
10.我市某校开展了以“梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品.现将从中挑选的50件参赛作品的成绩(单位:分)统计如下:
请根据上表提供的信息,解答下列问题:
(1)表中x的值为4,y的值为0.68;(直接填写结果)
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3…表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为$\frac{1}{6}$.(直接填写结果)
| 等级 | 成绩(用m表示) | 频数 | 频率 |
| A | 90≤m≤100 | x | 0.08 |
| B | 80≤m<90 | 34 | y |
| C | m<80 | 12 | 0.24 |
| 合计 | 50 | 1 |
(1)表中x的值为4,y的值为0.68;(直接填写结果)
(2)将本次参赛作品获得A等级的学生依次用A1、A2、A3…表示.现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,则恰好抽到学生A1和A2的概率为$\frac{1}{6}$.(直接填写结果)
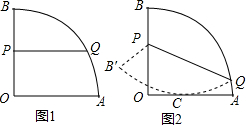 如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点.
如图,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是弧AB上的一动点. 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).