题目内容
1．计算：$\frac{1}{x-1}$-$\frac{1}{1+x}$-$\frac{2}{1+{x}^{2}}$-$\frac{4}{1+{x}^{4}}$+$\frac{8}{1-{x}^{8}}$．分析 原式通分并利用同分母分式的加减法则计算即可得到结果．
解答 解：原式=$\frac{-1-x-1+x}{1-{x}^{2}}$-$\frac{2}{1+{x}^{2}}$-$\frac{4}{1+{x}^{4}}$+$\frac{8}{1-{x}^{8}}$=$\frac{-2-2{x}^{2}-2+2{x}^{2}}{1-{x}^{4}}$-$\frac{4}{1+{x}^{4}}$+$\frac{8}{1-{x}^{8}}$=$\frac{-4-4{x}^{4}-4+4{x}^{4}}{1-{x}^{8}}$+$\frac{8}{1-{x}^{8}}$=0．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
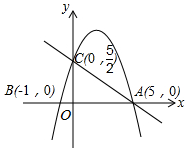如图，在平面直角坐标系中，已知抛物线y=ax2+bx+c与x轴交于A（5，0），B（-1，0）两点，与y轴交于点C（0，$\frac{5}{2}$）．
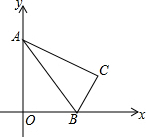如图，在平面直角坐标系中，点A的坐标为（0，$\sqrt{3}$），点B的坐标为（1，0），将△AOB沿直线AB折叠，点O在点C处，则点C的坐标为（$\frac{3}{2}$，$\frac{\sqrt{3}}{2}$）．
你能将-4、-3、-2、-1、0、1、2、3、4这9个数分别填入如图所示的幻方的9个空格中，使得处于同一行、同一列、同一对角线上的3个数相加都得0吗？