题目内容
8. 如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.
如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据正方形各内角为直角的性质,可以证明△ABE、△CBF、△DEF为直角三角形,分别求其斜边,即BE,EF,BF的值,根据边的长度和勾股定理的逆定理可以判定△BEF为直角三角形,即可解题.
解答 解:∵正方形各内角为直角,AB=4,AE=2,DF=1,
∴BC=CD=AD=AB=4,△ABE、△CBF、△DEF为直角三角形,DE=2,CF=3,
图中,BE2=AE2+AB2=22+42=20;
EF2=DE2+DF2=22+12=5,
BF2=BC2+CF2=42+32=25,
∴BE2+EF2=BF2,
即△BEF为直角三角形,
故图中有4个直角三角形.
故选:D.
点评 本题考查了勾股定理、勾股定理的逆定理;熟练掌握勾股定理,由勾股定理的逆定理证明△BEF是直角三角形是解题的关键.

练习册系列答案
相关题目
4.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
若A(m,y1),B(m-2,y2)两点都在该函数的图象上,当m=3时,y1=y2.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
18.用“加减法”将方程组$\left\{\begin{array}{l}{5x-3y=-5}\\{5x+4y=-1}\end{array}\right.$中的未知数x消去后得到的方程是( )
| A. | y=4 | B. | 7y=4 | C. | -7y=4 | D. | -7y=14 |
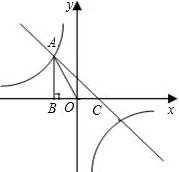 如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点$A(-\sqrt{3},2)$,过点A作AB⊥x轴于点B,连结AO.
如图,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点$A(-\sqrt{3},2)$,过点A作AB⊥x轴于点B,连结AO.
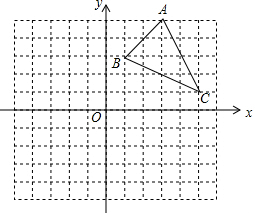 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).