题目内容
17.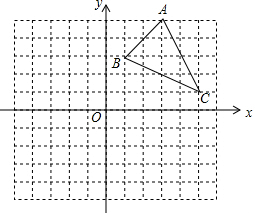 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).①画出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标;
②连结BC1,在坐标平面的格点上确定一个点P,使△B C1P是以B C1为底的等腰直角三角形,画出△B C1P,并写出所有P点的坐标.
分析 ①分别作出点A、B、C关于y轴的对称点,即可得△A1B1C1及C1的坐标;
②作出BC1的中垂线,在中垂线上根据勾股定理逆定理即可确定点P位置.
解答 解:①如图,△A1B1C1,即为所求作三角形,点C1的坐标为(-5,1);
②如图,点P的坐标为(-1,-1)或(-3,5).
点评 本题主要考查轴对称变换的作图及等腰直角三角形的性质,熟练掌握等腰直角三角形的性质与勾股定理逆定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列是二元一次方程的是( )
| A. | 2x-3=3x+1 | B. | xy-2=3 | C. | x+y=0 | D. | x2+2y=1 |
8. 如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.
如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.
 如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.
如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.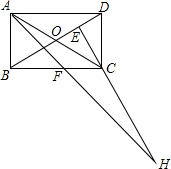 在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )
在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )
①AF=$\frac{1}{2}$FH;②BO=BF;③CA=CH;④BE=3ED.
 在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )
在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )①AF=$\frac{1}{2}$FH;②BO=BF;③CA=CH;④BE=3ED.
| A. | ②③ | B. | ③④ | C. | ①②④ | D. | ②③④ |
2. 如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为( )
如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为( )
 如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为( )
如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
9.2x3可以表示为( )
| A. | x3+x3 | B. | x3•x3 | C. | 2x•2x•2x | D. | 8x |
 如图,在四边形ABCD中,AD∥BC,要使△ABD≌△CDB,可添加一个条件为∠A=∠C.
如图,在四边形ABCD中,AD∥BC,要使△ABD≌△CDB,可添加一个条件为∠A=∠C.