��Ŀ����
13����ͼ����������ֽƬABCD�������²�����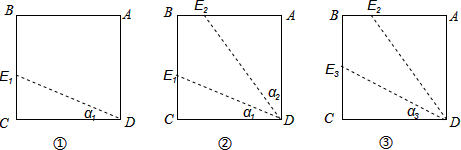
��1������D����һ��ֱ����BC���ཻ�ڵ�E1����ͼ�٣����ǡ�CDE1=a1��
��2������ADE1��ƽ���߽�AB���ڵ�E2����ͼ�ڣ����ǡ�ADE2=a2��
��3������CDE2��ƽ���߽�BC���ڵ�E3����ͼ�ۣ����ǡ�CDE3=a3��
���������Ӳ�����2�����ظ����ϲ��裬�õ�a1��a2������an�������������½��ۣ�
�ٵ�a1=10��ʱ��a2=40�㣻
��2a4+a3=90�㣻
�۵�a5=30��ʱ����CDE9�ա�ADE10��
�ܵ�a1=45��ʱ��BE2=$\sqrt{2}$AE2��
������ȷ�ĸ���Ϊ��������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �ٸ��ݽ�ƽ���ߵĶ�����㼴�ɣ�
�ڸ������⡢���ͼ�μ��㣻
�۸���ȫ�������ε��ж�����֤����
����E2F��BD��F�����ݵ���ֱ�������ε����ʵõ�BE2=$\sqrt{2}$FE2�����ݽ�ƽ���ߵ����ʵõ�AE2=FE2�������������ɣ�
��� �⣺�ٵ�a1=10��ʱ��a2=$\frac{90��-10��}{2}$=40�㣬����ȷ��
����ͼ�ۿ�֪��2a4+a3=90�㣬����ȷ��
�۵�a5=30��ʱ��a9=30�㣬a10=30�㣬
�ڡ�CDE9�͡�ADE10�У�
$\left\{\begin{array}{l}{��CD{E}_{9}=��AD{E}_{10}}\\{��C=��A}\\{DC=DA}\end{array}\right.$��
���CDE9�ա�ADE10������ȷ��
�ܵ�a1=45��ʱ����E1���B�غϣ�
��E2F��BD��F��
���ı���ABCD�������Σ�
���ABD=45�㣬
��BE2=$\sqrt{2}$FE2��
��DE2ƽ�֡�ADB��E2F��BD����A=90�㣬
��AE2=FE2��
��BE2=$\sqrt{2}$AE2������ȷ��
��ѡ��D��
���� ���⿼����������ε����ʡ���ƽ���ߵ����ʡ�ȫ�������ε��ж������ս�ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȡ�ȫ�������ε��ж������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
11������12��15��ʱ���ӱ��ϵ�ʱ��ͷ������ɵĽ��ǣ�������
| A�� | 90�� | B�� | 75�� | C�� | 82.5�� | D�� | 60�� |
12��ÿ�����£�����ط�������������ѩ����������裬���Dz������ţ��ݲⶨ��������ά��ֱ��ԼΪ0.0000105m������ֵ�ÿ�ѧ��������ʾΪ��������
| A�� | 1.05��105 | B�� | 0.105��10-4 | C�� | 1.05��10-5 | D�� | 105��10-7 |
5��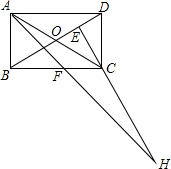 �ھ���ABCD�У�AB=1��AD=$\sqrt{3}$��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF��EC���ڵ�H�����н�������ȷ���ǣ�������
�ھ���ABCD�У�AB=1��AD=$\sqrt{3}$��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF��EC���ڵ�H�����н�������ȷ���ǣ�������
��AF=$\frac{1}{2}$FH����BO=BF����CA=CH����BE=3ED��
 �ھ���ABCD�У�AB=1��AD=$\sqrt{3}$��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF��EC���ڵ�H�����н�������ȷ���ǣ�������
�ھ���ABCD�У�AB=1��AD=$\sqrt{3}$��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF��EC���ڵ�H�����н�������ȷ���ǣ���������AF=$\frac{1}{2}$FH����BO=BF����CA=CH����BE=3ED��
| A�� | �ڢ� | B�� | �ۢ� | C�� | �٢ڢ� | D�� | �ڢۢ� |
2�� ��ͼ���ڡ�ABC�У���ACB=90�㣬BC=AC=4��MΪAB�е㣬D������BC��һ���㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90��õ��߶�AE������ED��ME����D���˶�������ME����СֵΪ��������
��ͼ���ڡ�ABC�У���ACB=90�㣬BC=AC=4��MΪAB�е㣬D������BC��һ���㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90��õ��߶�AE������ED��ME����D���˶�������ME����СֵΪ��������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬BC=AC=4��MΪAB�е㣬D������BC��һ���㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90��õ��߶�AE������ED��ME����D���˶�������ME����СֵΪ��������
��ͼ���ڡ�ABC�У���ACB=90�㣬BC=AC=4��MΪAB�е㣬D������BC��һ���㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90��õ��߶�AE������ED��ME����D���˶�������ME����СֵΪ��������| A�� | 2 | B�� | 2$\sqrt{2}$ | C�� | 4 | D�� | 4$\sqrt{2}$ |
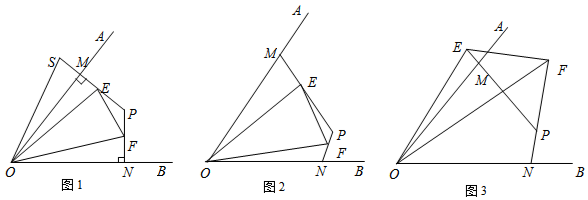
 ��ͼ����������ABCD�У�ȡAB=4��AE=2��DF=1��ͼ�й���ֱ�������Σ�����������
��ͼ����������ABCD�У�ȡAB=4��AE=2��DF=1��ͼ�й���ֱ�������Σ�����������