题目内容
20.若32m=5,3n=10,则34m-2n+1=$\frac{9}{4}$.分析 逆运用同底数幂相除,底数不变指数相减;同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘进行计算即可得解.
解答 解:34m-2n+1=34m÷32n×3,
=(32m)2÷(3n)2×3,
=52÷102×3,
=25÷100×9,
=$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查了同底数幂的除法,同底数幂的乘法,幂的乘方的性质,是基础题,熟记性质并灵活运用是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
18.“埃博拉”病毒是引起人类和灵长类动物发生埃博拉出血热(EBHF)的烈性病毒,科学家研究发现这种病毒粒子一般直径约为0.00000008m,0.00000008m用科学记数法表示为8×10-8m.
8. 如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.
如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.
 如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.
如图,在正方形ABCD中,取AB=4,AE=2,DF=1,图中共有直角三角形( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.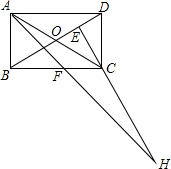 在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )
在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )
①AF=$\frac{1}{2}$FH;②BO=BF;③CA=CH;④BE=3ED.
 在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )
在矩形ABCD中,AB=1,AD=$\sqrt{3}$,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中正确的是( )①AF=$\frac{1}{2}$FH;②BO=BF;③CA=CH;④BE=3ED.
| A. | ②③ | B. | ③④ | C. | ①②④ | D. | ②③④ |
9.2x3可以表示为( )
| A. | x3+x3 | B. | x3•x3 | C. | 2x•2x•2x | D. | 8x |
9.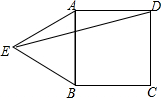 如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )
如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )
 如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )
如图,点E是正方形ABCD外一点,EA=4,EB=3,且∠AEB=45°,则ED的长为( )| A. | $\sqrt{23}$ | B. | 2$\sqrt{10}$ | C. | $\sqrt{41}$ | D. | 5$\sqrt{2}$ |

 如图,在四边形ABCD中,AD∥BC,要使△ABD≌△CDB,可添加一个条件为∠A=∠C.
如图,在四边形ABCD中,AD∥BC,要使△ABD≌△CDB,可添加一个条件为∠A=∠C.