题目内容
7.如图甲,Rt△ABC≌Rt△CDE,且∠ABC=∠EDC=90°,B,C,D三点共线,又点F为AE中点.(1)求证:△BDF为等腰直角三角形;
(2)若B,C,D所在直线经点C旋转成如图乙,其他条件不变,△BDF还是等腰直角三角形吗?说明理由.
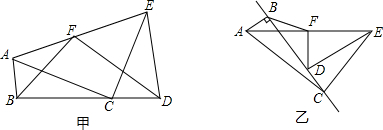
分析 (1)如图甲中,延长BF交DE的延长线于M,先证明△ABF≌△MEF,再证明△BDM是等腰直角三角形,由此可以得出结论.
(2)证明方法类似(1)略.
解答 (1)证明:如图甲中,延长BF交DE的延长线于M.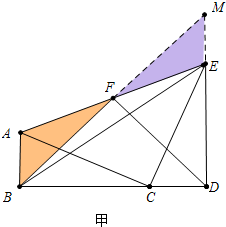
∵∠ABC=∠EDC=90°,B,C,D三点共线,
∴∠ABC+∠BDE=180°,
∴AB∥ED,
∴∠BAF=∠MEF,
在△ABF和△EMF中,
$\left\{\begin{array}{l}{∠BAF=∠MEF}\\{∠AFB=∠MFE}\\{AF=FE}\end{array}\right.$,
∴△ABF≌△MEF,
∴AB=ME,BF=MF
∵Rt△ABC≌Rt△CDE,
∴AB=CD,BC=DE
∴BD=DM,
∵∠BDM=90°,BF=FM,
∴FB=FD=FM,∠B=∠M=∠BDF=∠MDF=45°,
∴∠BFD=90°,
∴△FBD是等腰直角三角形.
(2)△FBD是等腰三角形.
证明如图乙中,延长BF交DE于M
∵∠ABC=∠EDC=∠BDE=90°
∴AB∥ED,
∴∠BAF=∠MEF,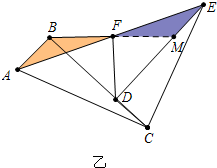
在△ABF和△EMF中,
$\left\{\begin{array}{l}{∠BAF=∠MEF}\\{∠AFB=∠MFE}\\{AF=FE}\end{array}\right.$,
∴△ABF≌△MEF,
∴AB=ME,BF=MF
∵Rt△ABC≌Rt△CDE,
∴AB=CD,BC=DE,
∴BC-CD=DE-EM,即BD=DM,
∵∠BDM=90°,BF=FM,
∴FB=FD=FM,∠B=∠M=∠BDF=∠MDF=45°,
∴∠BFD=90°,
∴△FBD是等腰直角三角形.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
16.若$\frac{1}{2}$m+1与m-2互为相反数,则m的值为( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
 已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?
已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?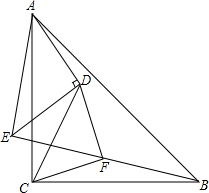 如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.
如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.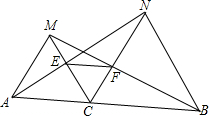 如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF.
如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF.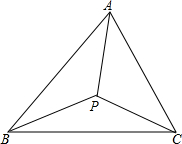 如图,P是△ABC内一点,PB=PC,∠PBA=∠PCA,求证:AP平分∠BAC.
如图,P是△ABC内一点,PB=PC,∠PBA=∠PCA,求证:AP平分∠BAC.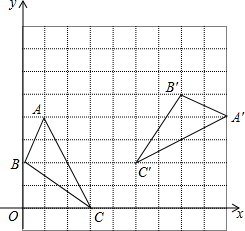 如图所示,在直角坐标系中,△A′B′C′是由△ABC绕点P旋转一定的角度而得,其中A(1,4),B(0,2),C(3,0),则旋转中心点P的坐标是(5,0).
如图所示,在直角坐标系中,△A′B′C′是由△ABC绕点P旋转一定的角度而得,其中A(1,4),B(0,2),C(3,0),则旋转中心点P的坐标是(5,0).