题目内容
14. 已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?
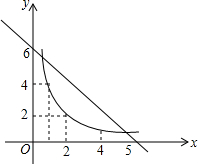
已知矩形A的长、宽分别是2和1,是否存在另一个矩形B,它的周长和面积分别是矩形A的周长和面积的2倍?对上述问题,小明同学从“图形”的角度,利用函数图象给予了解决.小明论证的过程开始是这样的:如果用x、y分别表示矩形的长和宽,那么矩形B满足x+y=6,xy=4.请你在如图所示的平面直角坐标系中画出矩形B满足的两个函数表达式的图象,并按照小明的论证思路完成后面的论证过程.
分析 设所求矩形的长为x、宽为y,表示出有关周长和面积的两个函数关系式,画出函数的图象,利用函数的图形判断是否存在这样的矩形即可.
解答 解:存在,
设所求矩形的长为x、宽为y,
∵已知矩形的长和宽分别是2和1,新矩形的周长和面积分别是已知矩形周长和面积的2倍,
∴2(x+y)=2×2×(2+1),xy=2×2×1
∴y=-x+6,y=$\frac{4}{x}$,
画出函数的图象如图,
根据图象知函数的图象有交点,所以存在两个矩形,能使得新矩形是原矩形的周长与面积的2倍.
点评 本题考查了反比例函数的应用,解题的关键是会灵活的运用函数图象交点的意义,以及图象的特点,试题中贯穿了方程思想和数形结合的思想,请注意体会.

练习册系列答案
相关题目
4.若分式方程$\frac{x}{x+2}=\frac{m}{x+2}$无解,则m的值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
5.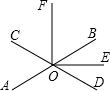 如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )
如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )
 如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )
如图,直线AB与CD相交于点O,OE平分∠BOD,OE⊥OF,若∠AOC=50°,则∠BOF的度数是( )| A. | 50° | B. | 75° | C. | 65° | D. | 55° |
2.如图,是舟山-嘉兴的高速公路示意图,王老师驾轿车从舟山出发,上高速公路途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了20千米/小时,比去时少用了1小时回到舟山.

(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见表:
我省交通部门规定:轿车的高速公路通行费w(元)的计算方法为:w=am+b+5,其中a元/(千米)为高速公路里程费,m(千米)为高速公路里程数(不包括跨海大桥长),b(元)为跨海大桥过桥费.若王老师从舟山到嘉兴所花的高速公路通行费为277.4元,求轿车的高速公路里程费a.

(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见表:
| 大桥名称 | 舟山跨海大桥 | 杭州湾跨海大桥 |
| 大桥长度 | 48千米 | 36千米 |
| 过桥费 | 100元 | 80元 |
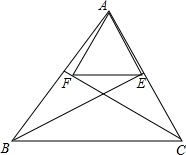 如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC.
如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC.