题目内容
12.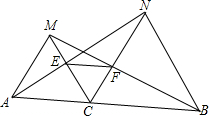 如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF.
如图,点C为线段AB上一点,△ACM、CBN为等边三角形,AN、CM交于E,BM、CN交于F,联结EF.(1)说明△CAN≌△CMB;
(2)说明△CEF为等边三角形.
分析 (1)由等边三角形可得其对应线段相等,对应角相等,进而可由SAS得到△CAN≌△CMB,结论得证;
(2)由(1)中的全等可得∠CAN=∠CMB,进而得出∠MCF=∠ACE,由ASA得出△CAE≌△CMF,即CE=CF,又ECF=60°,所以△CEF为等边三角形.
解答 证明:(1)∵△ACM,△CBN是等边三角形,
∴AC=MC,BC=NC,∠ACM=∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,即∠ACN=∠MCB,
在△CAN和△CMB中,
∵$\left\{\begin{array}{l}{AC=MC}\\{∠ACN=∠MCB}\\{NC=BC}\end{array}\right.$,
∴△CAN≌△CMB(SAS);
(2)∵△CAN≌△CMB,
∴∠CAN=∠CMB,
又∵∠MCF=180°-∠ACM-∠NCB=180°-60°-60°=60°,
∴∠MCF=∠ACE,
在△CAE和△CMF中,
∵$\left\{\begin{array}{l}{∠CAE=∠CMF}\\{CA=CM}\\{∠ACE=∠MCF}\end{array}\right.$,
∴△CAE≌△CMF(ASA),
∴CE=CF,
∴△CEF为等腰三角形,
又∵∠ECF=60°,
∴△CEF为等边三角形.
点评 本题主要考查了全等三角形的判定及性质以及等边三角形的判定问题,能够掌握全等三角形的判定方法是解题关键.

练习册系列答案
相关题目
1.PM2.5指标被纳入今年2月29日国务院批准发布的《环境空气质量标准》.根据该标准,PM2.5一级标准限值为日平均0.000035克/立方米,这一数据用科学记数法表示为( )克/立方米.
| A. | 3.5×10-5 | B. | 3.5×10-4 | C. | 0.35×10-4 | D. | 3.5×10-6 |
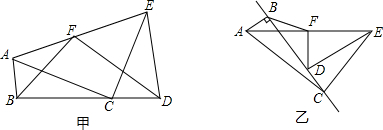
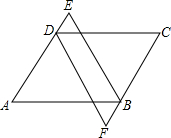 如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.
如图,已知AB=CD,AD=BC,DE=BF,说明BE=DF.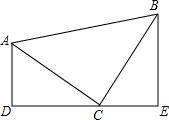 已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.
已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.