题目内容
12.若(y-4)(y+m)=y2+ny+8,则m+n的值为-8.分析 直接利用多项式乘以多项式运算法则进而得出m,n的等式求出答案.
解答 解:∵(y-4)(y+m)=y2+ny+8,
∴y2+(m-4)y-4m=y2+ny+8,
∴$\left\{\begin{array}{l}{m-4=n}\\{-4m=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-2}\\{n=-6}\end{array}\right.$,
则m+n的值为:-8.
故答案为:-8.
点评 此题主要考查了多项式乘以多项式,正确得出关于m,n的值是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
2.如图,是舟山-嘉兴的高速公路示意图,王老师驾轿车从舟山出发,上高速公路途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了20千米/小时,比去时少用了1小时回到舟山.

(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见表:
我省交通部门规定:轿车的高速公路通行费w(元)的计算方法为:w=am+b+5,其中a元/(千米)为高速公路里程费,m(千米)为高速公路里程数(不包括跨海大桥长),b(元)为跨海大桥过桥费.若王老师从舟山到嘉兴所花的高速公路通行费为277.4元,求轿车的高速公路里程费a.

(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见表:
| 大桥名称 | 舟山跨海大桥 | 杭州湾跨海大桥 |
| 大桥长度 | 48千米 | 36千米 |
| 过桥费 | 100元 | 80元 |
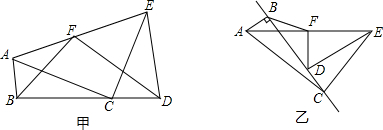
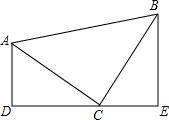 已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.
已知,如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥DE于D,BE⊥DE于E,若AD=2cm,BE=3cm,求DE的长.