题目内容
13.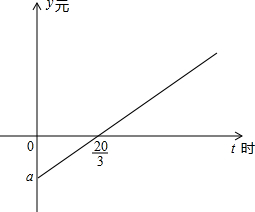 某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.
某市出租车通常采用如下运营模式:个体司机向出租车公司租借车辆运营,每天向公司上交一点量的“份子钱”,公司靠收每辆出租车的“份子钱”盈利,据了解,个体司机每运营一小时,平均可得“营业额”50元,但要支付“燃气费”20元,如图是某司机一天运营收益(除去“份子钱”和“燃气费”),y元随运营时间t时变化的函数图象.(1)求a的值及函数解析式;
(2)据统计,个体司机的运营收益率达到$\frac{1}{3}$,其“幸福指数”会达标,那么他需要运营几小时?(收益率=$\frac{营业额-份子钱-燃气费}{营业额}$)
(3)出租车公司为了改变效益,决定调整“分子钱”,据市场调查可知,出租车数量s(辆)与“分子钱”的增加额b(元)之间的关系为s=-$\frac{1}{2}$b+160.若调整时必须保证个体司机在运营12小时时,收益率不低于$\frac{1}{5}$,那么增加额b为多少元时,公司效益最高?
分析 (1)由图象可得,t=$\frac{20}{3}$时,y=0,设份子钱为m元,根据题意得$\frac{20}{3}×50-\frac{20}{3}×20-m=0$,解得:m=200,即可确定a的值,再利用待定系数法求互相解析式.
(2)设他需要运营x小时,根据收益率列出方程,即可解答.
(3)先根据调整时必须保证个体司机在运营12小时时,收益率不低于$\frac{1}{5}$,求出b的取值范围,再设公司效益为W元,表示出W,根据二次函数的性质和b的取值范围,确定b的值即可.
解答 解:(1)由图象可得,t=$\frac{20}{3}$时,y=0,
设份子钱为m元,
∴$\frac{20}{3}×50-\frac{20}{3}×20-m=0$
解得:m=200,
∴a=-200,
设函数解析式为:y=kt+b,
把(0,-200),($\frac{20}{3}$,0)代入得:$\left\{\begin{array}{l}{b=-200}\\{\frac{20}{3}k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=30}\\{b=-200}\end{array}\right.$,
∴y=30t-200.
(2)设他需要运营x小时,根据题意可得:
$\frac{50x-200-20x}{50x}=\frac{1}{3}$,
解得:x=15,
经检验,x=15是原方程的解,
∴他需要运营15小时.
(3)∵调整时必须保证个体司机在运营12小时时,收益率不低于$\frac{1}{5}$,
∴$\frac{50×12-(200+b)-12×20}{50×12}≥\frac{1}{5}$
解得:b≤40,
∴0≤b≤40,
设公司效益为W元,
则W=$(-\frac{1}{2}b+160)(200+b)$=$-\frac{1}{2}(b-60)^{2}+33800$,
∵0≤b≤40,
∴当b=40时,W有最大值,最大为=$-\frac{1}{2}(40-60)^{2}+33800$=33600,
∴增加额b为40元时,公司效益最高.
点评 本题考查了一次函数的应用,解决本题的关键是读懂函数图象,结合题目所给的条件,列出方程和不等式.

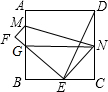 如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
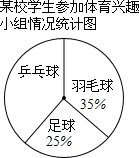 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )| A. | 25人 | B. | 35人 | C. | 40人 | D. | 100人 |
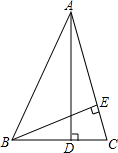 已知:△ABC中,AD⊥BC,BE⊥AC交AD于点F,若∠BAC=45°,CD=1,BD=$\frac{3}{2}$,求AD的长.
已知:△ABC中,AD⊥BC,BE⊥AC交AD于点F,若∠BAC=45°,CD=1,BD=$\frac{3}{2}$,求AD的长.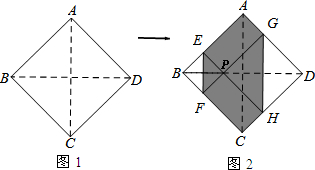
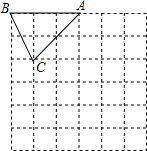 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1. 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1.