题目内容
已知方程组
和方程组
的解相同,求2(a+b)2014的值.
|
|
考点:二元一次方程组的解
专题:
分析:根据方程组的解相同,可得新方程组,根据解方程组,可得方程组的解,根据方程组的解满足方程,把解代入,可得关于a、b的方程组,根据解方程组,可得a、b的值,根据乘方,可得幂.
解答:解;方程组
和方程组
的解相同,
可得
,
解第一个方程组得
,
把
代入第二个方程组得
,
解得
2(a+b)2014=2(
-
)2014
=2.
|
|
可得
|
|
解第一个方程组得
|
把
|
|
解得
|
2(a+b)2014=2(
| 1 |
| 2 |
| 3 |
| 2 |
=2.
点评:本题考查了二元一次方程组的解,先组合成新的方程组,分别求出两个方程组的解,最后求幂.

练习册系列答案
相关题目
无论x取何值下列不等式一定成立的是( )
| A、x≥-x |
| B、x≤-x |
| C、x-1<x |
| D、x2>x |
 已知两个不等式的解集在数轴上如图,那么这个解集为( )
已知两个不等式的解集在数轴上如图,那么这个解集为( )| A、x<-1 | B、x≤2 |
| C、-1<x≤2 | D、x≤-1 |
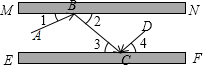 如图,MN、EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
如图,MN、EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律: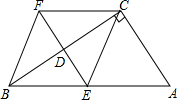 已知:如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
已知:如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE. 如图,直线AC∥BD,直线AB分别与它们相交于A,B,三条直线把平面分成①②③④⑤⑥六个部分(每个部分不包括边界).当动点P落在某个部分时,连结PA,PB,构成∠PAC,∠APB,∠PBD三个角.
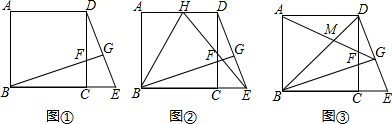
如图,直线AC∥BD,直线AB分别与它们相交于A,B,三条直线把平面分成①②③④⑤⑥六个部分(每个部分不包括边界).当动点P落在某个部分时,连结PA,PB,构成∠PAC,∠APB,∠PBD三个角. 如图,在平行四边形ABCD中,延长CD到E,使DE=DC,连接BE交AD于F,交AC于G.
如图,在平行四边形ABCD中,延长CD到E,使DE=DC,连接BE交AD于F,交AC于G.