题目内容
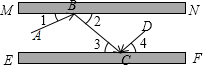 如图,MN、EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
如图,MN、EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;写出作图过程.
(2)试判断AB与CD的位置关系,并说明理由.
(3)线段BC上有一点P,过P点作直线交EF于点G,当∠BPG=2∠2时,探究直线PG与AB的位置关系.
考点:平行线的判定与性质
专题:应用题
分析:(1)根据折射线与反射线的关系,作出∠2=∠BCE=∠DCF即可得到反射光线CD;
(2)由∠1=∠2,根据平角的定义得到∠ABC=180°-2∠2,由∠3=∠4,根据等角的余角相等得∠BCE=∠DCF,再根据平角的定义得到∠BCD=180°-2∠BCE,由于MN∥EF,根据两直线平行,内错角相等得到∠2=∠BCE,利用等量代换有∠ABC=∠BCD,然后根据内错角相等,两直线平行可得AB∥CD;
(3)求出∠ABC+∠BPG=180°,根据平行线的判定推出即可.
(2)由∠1=∠2,根据平角的定义得到∠ABC=180°-2∠2,由∠3=∠4,根据等角的余角相等得∠BCE=∠DCF,再根据平角的定义得到∠BCD=180°-2∠BCE,由于MN∥EF,根据两直线平行,内错角相等得到∠2=∠BCE,利用等量代换有∠ABC=∠BCD,然后根据内错角相等,两直线平行可得AB∥CD;
(3)求出∠ABC+∠BPG=180°,根据平行线的判定推出即可.
解答:解:(1)解:(1)如图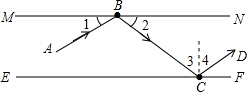 ,用量角器作∠BCE,再作∠DCF=∠BCE,∠3=∠4,BC和CD在MN和EF之间,则CD为所求;
,用量角器作∠BCE,再作∠DCF=∠BCE,∠3=∠4,BC和CD在MN和EF之间,则CD为所求;
(2)AB与CD的平行,
理由如下:∵∠1=∠2,
∴∠ABC=180°-2∠2,
∵光线BC经镜面EF反射后的反射光线CD,
∴∠3=∠4,
∴∠BCE=∠DCF,
∴∠BCD=180°-2∠BCE,
∵MN∥EF,
∴∠2=∠BCE,
∴∠ABC=∠BCD,
∴AB∥CD;
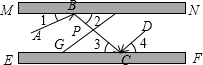
(3)PG∥AB,
理由是:∵∠ABC+2∠2=180°,∠BPG=2∠2,
∴∠ABC+∠BPG=180°,
∴PG∥AB.
 ,用量角器作∠BCE,再作∠DCF=∠BCE,∠3=∠4,BC和CD在MN和EF之间,则CD为所求;
,用量角器作∠BCE,再作∠DCF=∠BCE,∠3=∠4,BC和CD在MN和EF之间,则CD为所求;(2)AB与CD的平行,
理由如下:∵∠1=∠2,
∴∠ABC=180°-2∠2,
∵光线BC经镜面EF反射后的反射光线CD,
∴∠3=∠4,
∴∠BCE=∠DCF,
∴∠BCD=180°-2∠BCE,
∵MN∥EF,
∴∠2=∠BCE,
∴∠ABC=∠BCD,
∴AB∥CD;

(3)PG∥AB,
理由是:∵∠ABC+2∠2=180°,∠BPG=2∠2,
∴∠ABC+∠BPG=180°,
∴PG∥AB.
点评:本题考查了平行线的性质和判定的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.

练习册系列答案
相关题目
在-
,
,
,0.3030030003,-
,3.14,(
)2中有理数的个数是( )
| π |
| 3 |
|
| ||
| 2 |
| 23 |
| 7 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列方程中,是二元一次方程的有( )
A、
| ||||
B、
| ||||
| C、y=-3x-2 | ||||
| D、mn+m=7 |
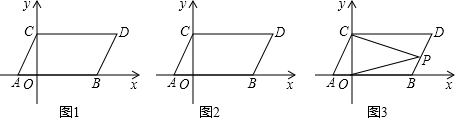
 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,