题目内容
 如图,在平行四边形ABCD中,延长CD到E,使DE=DC,连接BE交AD于F,交AC于G.
如图,在平行四边形ABCD中,延长CD到E,使DE=DC,连接BE交AD于F,交AC于G.(1)若BE为∠ABC的平分线,求证:BC=AF+DE;
(2)若BC=2AB,DE=1,∠ABC=60°,求GF的长.
考点:平行四边形的性质
专题:
分析:(1)由在平行四边形ABCD中,BE为∠ABC的平分线,易证得△ABF与△BCE是等腰三角形,然后由平行四边形的性质,即可证得BC=AF+DE;
(2)由BC=2AB,DE=1,∠ABC=60°,可得BF是角平分线,△ABG是含30°角的直角三角形的性质,然后由△AGF∽△CGB,根据相似三角形的对应边成比例,即可求得答案.
(2)由BC=2AB,DE=1,∠ABC=60°,可得BF是角平分线,△ABG是含30°角的直角三角形的性质,然后由△AGF∽△CGB,根据相似三角形的对应边成比例,即可求得答案.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=CD,
∴∠AFB=∠CBF,
∵BE为∠ABC的平分线,
∴∠ABF=∠CBF,
∴∠AFB=∠ABF,
∴AF=AB,
∴CD=AF,
同理:BC=CE,
∴BC=CE=CD+DE=AF+DE;
(2)在BC上截取BN=AB=1,连接AN,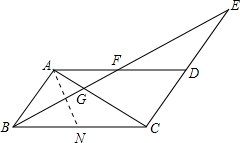
∵∠ABC=60°,
∴△ANB是等边三角形,
∴AN=1=BN,∠ANB=∠BAN=60°,
∵BC=2AB=2,
∴CN=1=AN,
∴∠ACN=∠CAN=
×60°=30°,
∴∠BAC=90°.
∴∠CBF=∠E=30°,
∴∠ABF=∠CBF=30°,
∴BG=
=
,
∴AF=AB=DE=1,BC=2AB=2DE=2,
∵△AGF∽△CGB,
∴GF:BG=AF:BC=1:2,
∴GF=
.
∴AD∥BC,AD=CD,
∴∠AFB=∠CBF,
∵BE为∠ABC的平分线,
∴∠ABF=∠CBF,
∴∠AFB=∠ABF,
∴AF=AB,
∴CD=AF,
同理:BC=CE,
∴BC=CE=CD+DE=AF+DE;
(2)在BC上截取BN=AB=1,连接AN,

∵∠ABC=60°,
∴△ANB是等边三角形,
∴AN=1=BN,∠ANB=∠BAN=60°,
∵BC=2AB=2,
∴CN=1=AN,
∴∠ACN=∠CAN=
| 1 |
| 2 |
∴∠BAC=90°.
∴∠CBF=∠E=30°,
∴∠ABF=∠CBF=30°,
∴BG=
| AB |
| cos30° |
2
| ||
| 3 |
∴AF=AB=DE=1,BC=2AB=2DE=2,
∵△AGF∽△CGB,
∴GF:BG=AF:BC=1:2,
∴GF=
| ||
| 3 |
点评:此题考查了平行四边形的性质、相似三角形的对应边成比例、直角三角形的性质以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程中,是二元一次方程的有( )
A、
| ||||
B、
| ||||
| C、y=-3x-2 | ||||
| D、mn+m=7 |
 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,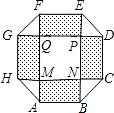 某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.
某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.