题目内容
如图,正方形ABCD中,E为BC延长线上一点,F为DC上一点,且CE=CF,连接BF并延长与DE交于点G.
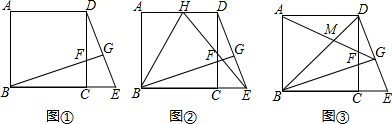
(1)如图①,求证:BG⊥DE;
(2)如图②,当点F为边CD的中点时,连接EF并延长交AD于点H,连接BH,求证:四边形BEDH是等腰梯形;
(3)如图③,点G是DE的中点时,连接BD、AG交于点M,求证:DE=
AM.

(1)如图①,求证:BG⊥DE;
(2)如图②,当点F为边CD的中点时,连接EF并延长交AD于点H,连接BH,求证:四边形BEDH是等腰梯形;
(3)如图③,点G是DE的中点时,连接BD、AG交于点M,求证:DE=
| 2 |
考点:四边形综合题
专题:
分析:(1)由正方形的性质就可以得出△BCF≌△DCE,就可以得出∠CBF=∠CDE,就可以得出∠BGE=90°而得出结论;
(2)通过证明△HDF≌△ECF就可以得出HD=CE=CF,由CF=
DC,就可以得出得出AH=DH=CE就可以得出△DCE≌△BAH就可以得出DE=BH,就可以得出结论;
(3)连结CG,由直角三角形的性质就可以得出△ADG≌△BCG,得出AG=BG就可以得出∠GAB=∠GBA,由BD=BE,BG⊥DE就可以得出∠DBG=∠EBG=∠CDE,就可以得出∠BDE=∠ABG=∠BAG,由△ABM∽△DBE就可以得出结论.
(2)通过证明△HDF≌△ECF就可以得出HD=CE=CF,由CF=
| 1 |
| 2 |
(3)连结CG,由直角三角形的性质就可以得出△ADG≌△BCG,得出AG=BG就可以得出∠GAB=∠GBA,由BD=BE,BG⊥DE就可以得出∠DBG=∠EBG=∠CDE,就可以得出∠BDE=∠ABG=∠BAG,由△ABM∽△DBE就可以得出结论.
解答:(1)证明:如图①,∵四边形ABCD是正方形,
∴AB=BC=CD=AD,AD∥BC,AB∥CD,∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴∠DCE=∠ABC=∠ADC=90°,
∴∠BCD=∠DCE.
在△BCF和△DCE中
,
∴△BCF≌△DCE(SAS),
∴∠BFC=∠E,∠CBF=∠CDE.
∵∠E+∠CDE=90°,
∴∠E+∠CBF=90°,
∴∠BGE=90°,
∴BG⊥DE;
(2)证明:如图②∵F为边CD的中点,
∴DF=CF=
CD.
∵AD∥BC,
∴∠DHF=∠CEF.
在△HDF和△ECF中
,
∴△HDF≌△ECF(AAS),
∴HD=CE,
∴HD=CF=
CD,
∴HD=
AD,
∴AH=HD,
∴AH=CE.
在△DCE和△BAH中
,
∴△DCE≌△BAH(SAS),
∴DE=BH.
∵AD∥BE,
∴四边形BEDH是等腰梯形;
(3)解:如图③,连结CG,
∵G是DE的中点,
∴CG=DG,
∴∠DCG=∠GDC,
∴∠ADG=∠BCG.
在△ADG和△BCG中
,
∴△ADG≌△BCG(SAS),
∴AG=BG,
∴∠GAB=∠GBA.
∵BG是△DBE的中线,BG⊥DE,
∴BD=BE,
∴∠DBG=∠EBG,
∴∠DBG=∠EBG=∠EDC.
∵四边形ABCD是正方形,
∴∠ABD=∠DBC=∠BDC=45°.
∴∠ABD+∠DBG=∠BDC+∠CDE,
∴∠ABG=∠BDE,
∴∠GAB=∠BDE.
∵∠ABD=∠DBC,
∴△ABM∽△DBE,
∴
=
.
∵四边形ABCD是正方形,
∴
=
,
∴
=
,
∴DE=
AM.
∴AB=BC=CD=AD,AD∥BC,AB∥CD,∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴∠DCE=∠ABC=∠ADC=90°,
∴∠BCD=∠DCE.
在△BCF和△DCE中
|
∴△BCF≌△DCE(SAS),
∴∠BFC=∠E,∠CBF=∠CDE.
∵∠E+∠CDE=90°,
∴∠E+∠CBF=90°,
∴∠BGE=90°,
∴BG⊥DE;
(2)证明:如图②∵F为边CD的中点,
∴DF=CF=
| 1 |
| 2 |
∵AD∥BC,
∴∠DHF=∠CEF.
在△HDF和△ECF中
|
∴△HDF≌△ECF(AAS),
∴HD=CE,
∴HD=CF=
| 1 |
| 2 |
∴HD=
| 1 |
| 2 |
∴AH=HD,
∴AH=CE.
在△DCE和△BAH中
|
∴△DCE≌△BAH(SAS),
∴DE=BH.
∵AD∥BE,
∴四边形BEDH是等腰梯形;
(3)解:如图③,连结CG,
∵G是DE的中点,
∴CG=DG,
∴∠DCG=∠GDC,
∴∠ADG=∠BCG.
在△ADG和△BCG中
|
∴△ADG≌△BCG(SAS),
∴AG=BG,
∴∠GAB=∠GBA.
∵BG是△DBE的中线,BG⊥DE,
∴BD=BE,
∴∠DBG=∠EBG,

∴∠DBG=∠EBG=∠EDC.
∵四边形ABCD是正方形,
∴∠ABD=∠DBC=∠BDC=45°.
∴∠ABD+∠DBG=∠BDC+∠CDE,
∴∠ABG=∠BDE,
∴∠GAB=∠BDE.
∵∠ABD=∠DBC,
∴△ABM∽△DBE,
∴
| AB |
| BD |
| AM |
| DE |
∵四边形ABCD是正方形,
∴
| BD |
| AB |
| 2 |
∴
| DE |
| AM |
| 2 |
∴DE=
| 2 |
点评:本题考查了矩形的性质的运用,全等三角形的判定及性质的运用,垂直的判定及性质的运用,等腰三角形的性质的运用,等腰三角形的判定及性质的运用,直角三角形的性质的运用,相似三角形的判定及性质的运用,解答时证明三角形相似是难点.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
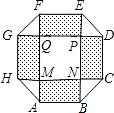 某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.
某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.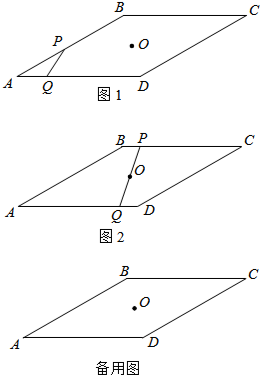 如图1,菱形ABCD中,∠A=30°,边长AB=10cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止,点Q沿2方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋连接,设t秒后橡皮筋扫过的面积为ycm2.
如图1,菱形ABCD中,∠A=30°,边长AB=10cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止,点Q沿2方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋连接,设t秒后橡皮筋扫过的面积为ycm2.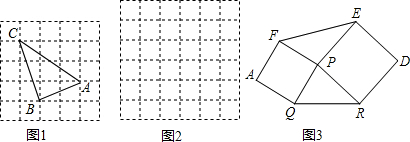
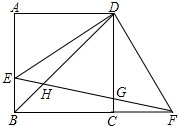 如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.