Question

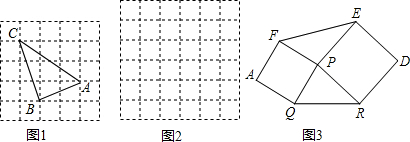
如图，直线AC∥BD，直线AB分别与它们相交于A，B，三条直线把平面分成①②③④⑤⑥六个部分（每个部分不包括边界）．当动点P落在某个部分时，连结PA，PB，构成∠PAC，∠APB，∠PBD三个角．
（1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；
（2）当动点P落在第②部分时，∠PAC，∠APB，∠PBD三者之间的数量关系是

 

；
（3）当动点P落在第③部分时，∠PAC，∠APB，∠PBD三者之间的数量关系是

 

；
（4）当动点P落在第④部分时，∠PAC，∠APB，∠PBD三者之间的数量关系是

 

．

Answer 1

考点：平行线的性质

专题：探究型

分析：（1）过点P作AC的平行线，交AB于点E，如图1，根据平行线的性质、传递性和等式的基本性质即可证明；
（2）过点P作EF∥AC，如图2，根据平行线的性质、传递性和等式的基本性质可得出∠APB+∠PAC+∠PBD=360°；
（3）如图3，根据平行线的性质、三角形外角的性质可得出∠PAC=∠APB+∠PBD；
（4）如图4，根据平行线的性质、三角形外角的性质可得出∠PAC+∠APB=∠PBD．

解答：（1）证明：过点P作AC的平行线，交AB于点E，如图1．
∵PE∥AC，AC∥BD，
∴PE∥BD，
∴∠PAC=∠APE，∠PBD=∠EPB，
∴∠APB=∠APE+∠EPB=∠PAC+∠PBD；

（2）解：∠APB+∠PAC+∠PBD=360°．理由如下：
过点P作EF∥AC，如图2，
因为AC∥BD，
所以EF∥BD，
所以∠BPF+∠PBD=180°．
同理∠APF+∠PAC=180°，
因此∠APF+∠BPF+∠PAC+∠PBD=360°，
即∠APB+∠PAC+∠PBD=360°；

（3）解：∠PAC=∠APB+∠PBD．理由如下：
如图3，∵AC∥BD，
∴∠PBD=∠PQC．
∵∠PAC=∠APB+∠PQC，
∴∠PAC=∠APB+∠PBD；

（4）解：∠PAC+∠APB=∠PBD．
如图4，∵AC∥BD，
∴∠PBD=∠PQC．
∵∠PAC+∠APB=∠PQC，
∴∠PAC+∠APB=∠PBD．
故答案为（2）∠APB+∠PAC+∠PBD=360°；
（3）∠PAC=∠PBD+∠APB；
（4）∠PAC=∠PBD+∠APB．

点评：本题考查了平行线的性质，三角形外角的性质以及数形结合思想的应用，是基础知识比较简单．