题目内容
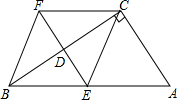 已知:如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
已知:如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.(1)
| BE |
| BA |
(2)试判断四边形BECF的形状,并说明理由;
(3)当∠A为多少度时,四边形BECF是正方形?画出草图,并证明你的结论.
考点:正方形的判定,菱形的判定
专题:
分析:(1)利用线段垂直平分线的性质以及平行线分线段成比例定理得出即可;
(2)利用四条边相等的四边形是菱形进而得出答案;
(3)利用等腰直角三角形的性质得出CE⊥AB,进而得出四边形BECF是正方形.
(2)利用四条边相等的四边形是菱形进而得出答案;
(3)利用等腰直角三角形的性质得出CE⊥AB,进而得出四边形BECF是正方形.
解答: 解:(1)∵BC的垂直平分线EF交BC于点D,
解:(1)∵BC的垂直平分线EF交BC于点D,
∴BD=CD,∠BDE=90°,
又∵∠ACB=90°,
∴DE∥AC,
∴BE=AE,
∴
的值为
,
故答案为:
;
(2)菱形;
理由:∵BE=AE,CF=AE,
∴FC=BE,
∵BC的垂直平分线EF交BC于点D,交AB于点E,
∴BF=FC,BE=EC,
∴BF=FC=BE=EC,
∴四边形BECF是菱形;
(3)当∠A为45°时,四边形BECF是正方形,
理由:∵∠A=45°,∠BCA=90°,
∴∠CBA=45°,
∴BC=AC,
∵BE=AE,
∴CE⊥BA,
∵四边形BECF是菱形,
∴四边形FBEC是正方形.
 解:(1)∵BC的垂直平分线EF交BC于点D,
解:(1)∵BC的垂直平分线EF交BC于点D,∴BD=CD,∠BDE=90°,
又∵∠ACB=90°,
∴DE∥AC,
∴BE=AE,
∴
| BE |
| BA |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
(2)菱形;
理由:∵BE=AE,CF=AE,
∴FC=BE,
∵BC的垂直平分线EF交BC于点D,交AB于点E,
∴BF=FC,BE=EC,
∴BF=FC=BE=EC,
∴四边形BECF是菱形;
(3)当∠A为45°时,四边形BECF是正方形,

理由:∵∠A=45°,∠BCA=90°,
∴∠CBA=45°,
∴BC=AC,
∵BE=AE,
∴CE⊥BA,
∵四边形BECF是菱形,
∴四边形FBEC是正方形.
点评:此题主要考查了菱形的判定方法以及正方形的判定和等腰直角三角形的性质等知识,熟练掌握菱形与正方形的判定方法是解题关键.

练习册系列答案
相关题目
顺次连结四边形各边中点所得的四边形是菱形,则原四边形的对角线必定( )
| A、垂直 | B、相等 |
| C、平分 | D、垂直平分 |
下列根式中,属于最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知A,B两点的坐标分别为(2,4),(7,2),
已知A,B两点的坐标分别为(2,4),(7,2),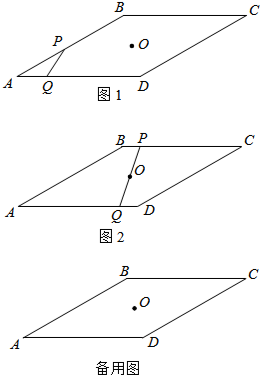 如图1,菱形ABCD中,∠A=30°,边长AB=10cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止,点Q沿2方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋连接,设t秒后橡皮筋扫过的面积为ycm2.
如图1,菱形ABCD中,∠A=30°,边长AB=10cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A→B→C方向以每秒2cm的速度运动,到点C停止,点Q沿2方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋连接,设t秒后橡皮筋扫过的面积为ycm2.