题目内容
14．
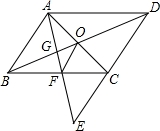如图，E是?ABCD的边DC延长线上的一点，且CE=DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于点O，连接OF，求证：AB=2OF．
分析 先证明△ABF≌△ECF得BF=FC，再利用三角形中位线定理即可解决问题．
解答 证明：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，AO=OC，
∵CD=CE，
∴AB=CE，∠BAF=∠CEF，
在△ABF和△ECF中，
$\left\{\begin{array}{l}{∠BAF=∠FEC}\\{∠AFB=∠EFC}\\{AB=CE}\end{array}\right.$，
∴△ABF≌△ECF，
∴BF=FC，
∵AO=OC，
∴AB=2OF．
点评 本题考查三角形中位线定理、平行四边形的性质、全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形，出现中点条件想到三角形中位线定理，属于中考常考题型．
练习册系列答案
相关题目
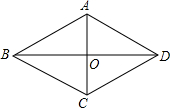如图，四边形ABCD是菱形，对角线AC、BD相交于O，如果菱形的周长是40cm，它的一条对角线AC长10cm，
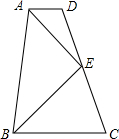如图，在梯形ABCD中，AD∥BC，E为CD的中点，AD+BC=AB．则：
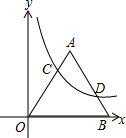在平面直角坐标系中，等边三角形OAB中OB在x轴上，点A在第一象限，双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C，交AB于点D，若OC：BD=2：1，则OB=5．
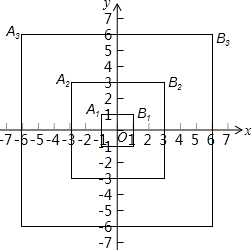如图，第一个正方形的顶点A1（-1，1），B1（1，1）；第二个正方形的顶点A2（-3，3），B2（3，3）；第三个正方形的顶点A3（-6，6），B3（6，6），按顺序取点A1，B2，A3，B4，A5，B6…，则第10个点应取点B10，其坐标为（55，55），第2n-1（n为正整数）个点应取点A2n-1，其坐标为（-n（2n-1），n（2n-1））．
如图，将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE，点M、N分别是BD、GE的中点，若BC=14，CE=2，则MN的长（ ）