题目内容
19.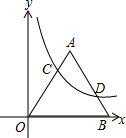 在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5.
在平面直角坐标系中,等边三角形OAB中OB在x轴上,点A在第一象限,双曲线y=$\frac{4\sqrt{3}}{x}$交OA于点C,交AB于点D,若OC:BD=2:1,则OB=5.
分析 作CE⊥x轴于E,DF⊥x轴于F,如图,利用等边三角形的性质∠COE=∠B=60°,设OE=t,利用含30度的直角三角形三边的关系得到CE=$\sqrt{3}$t,OC=2t,则C(t,$\sqrt{3}$t),再把C(t,$\sqrt{3}$t)代入y=$\frac{4\sqrt{3}}{x}$得t=2,所以OC=4,则BD=2,然后在Rt△BDF中可计算出BF=$\frac{1}{2}$BD=1,DF=$\sqrt{3}$BF=$\sqrt{3}$,利用反比例函数图象上点的坐标特征可求出D点坐标得到OF的长,然后计算OF+BF即可.
解答 解:作CE⊥x轴于E,DF⊥x轴于F,如图,
∵△AOB为等边三角形,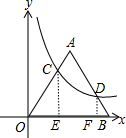
∴∠COE=∠B=60°,
设OE=t,则CE=$\sqrt{3}$t,OC=2t,
∴C(t,$\sqrt{3}$t),
把C(t,$\sqrt{3}$t)代入y=$\frac{4\sqrt{3}}{x}$得t•$\sqrt{3}$t=4$\sqrt{3}$,解得t1=-2(舍去),t2=2,
∴OC=4,
∵OC:BD=2:1,
∴BD=2,
在Rt△BDF中,BF=$\frac{1}{2}$BD=1,DF=$\sqrt{3}$BF=$\sqrt{3}$,
当y=$\sqrt{3}$时,$\frac{4\sqrt{3}}{x}$=$\sqrt{3}$,解得x=4,
∴OF=4,
∴OB=OF+BF=4+1=5.
故答案为5.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了等边三角形的性质.

练习册系列答案
相关题目
4.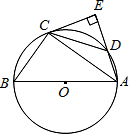 如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=10,AC=8,求tan∠DCE的值.
 如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.(1)求证:DC=BC;
(2)若AB=10,AC=8,求tan∠DCE的值.
11.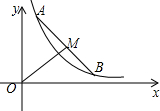 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$-1 |
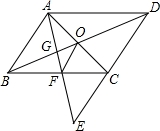 如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.
如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.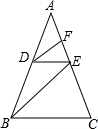 已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.
已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.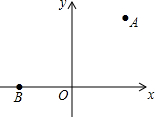 如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).
如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).