题目内容
3.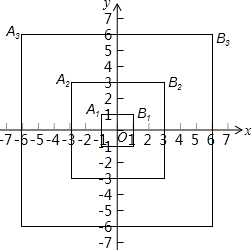 如图,第一个正方形的顶点A1(-1,1),B1(1,1);第二个正方形的顶点A2(-3,3),B2(3,3);第三个正方形的顶点A3(-6,6),B3(6,6),按顺序取点A1,B2,A3,B4,A5,B6…,则第10个点应取点B10,其坐标为(55,55),第2n-1(n为正整数)个点应取点A2n-1,其坐标为(-n(2n-1),n(2n-1)).
如图,第一个正方形的顶点A1(-1,1),B1(1,1);第二个正方形的顶点A2(-3,3),B2(3,3);第三个正方形的顶点A3(-6,6),B3(6,6),按顺序取点A1,B2,A3,B4,A5,B6…,则第10个点应取点B10,其坐标为(55,55),第2n-1(n为正整数)个点应取点A2n-1,其坐标为(-n(2n-1),n(2n-1)).
分析 根据选点的规律,罗列出部分点的坐标,根据这些点的坐标找出规律“A2n-1(-n(2n-1),n(2n-1)),B2n(n(2n+1),n(2n+1))(n为正整数)”,再根据该规律解决问题.
解答 解:观察,发现规律:A1(-1,1),B2(3,3),A3(-6,6),B4(10,10),A5(-15,15),…,
∴A2n-1(-n(2n-1),n(2n-1)),B2n(n(2n+1),n(2n+1))(n为正整数).
∵10=2×5,
∴B10(5×(10+1),5×(10+1))=(55,55).
故答案为:(55,55);A2n-1;(-n(2n-1),n(2n-1)).
点评 本题考查了规律型中的点的坐标,解题的关键是找出规律“A2n-1(-n(2n-1),n(2n-1)),B2n(n(2n+1),n(2n+1))(n为正整数)”.本题属于中档题,难度不大,解决该题型题目时,根据选点的规律列出部分点的坐标,根据这些点的坐标发现规律是关键.

练习册系列答案
相关题目
11.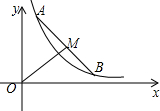 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$-1 |
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
15.与$\sqrt{3}$+1最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.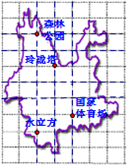 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
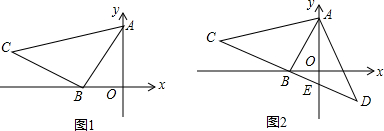
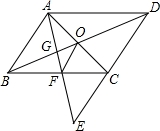 如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.
如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.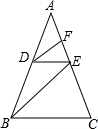 已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.
已知,如图,在△ABC中,D是AB上一点,且AD:DB=3:2,DE∥BC,AC于点E,DF∥BE,交AC于点F,若AF=9,求FE、EC的长.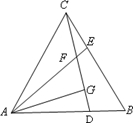 如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.