题目内容
6.在等腰三角形ABC中,AB=AC=5,BC=6,D是BC上一点,作DE⊥AB,DF⊥AC,则DE+DF=4.分析 首先求得AB上的高为h,连接AD,则△ABD的面积+△ACD的面积=△ABC的面积,得出$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$AB•h,再由AB=AC,得出DE+DF=h即可.
解答 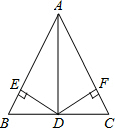 证明:设AB上的高为h,
证明:设AB上的高为h,
则h=$\sqrt{{5}^{2}-{3}^{2}}$=4,
则△ABD的面积+△ACD的面积=△ABC的面积,
∵△ABD的面积=$\frac{1}{2}$AB•DE,△ACD的面积=$\frac{1}{2}$AC•DF,△ABC的面积=$\frac{1}{2}$AB•h,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=$\frac{1}{2}$BC•h,
又∵AB=AC
∴DE+DF=$\frac{6}{5}$h=4.8.
故答案为:4.8.
点评 本题考查了等腰三角形的性质、三角形面积的计算方法;熟练掌握等腰三角形的性质,由三角形ABC面积的计算方法得出结论是解决问题的关键.

练习册系列答案
相关题目
1.下列各组中的两项,不是同类项的是( )
| A. | 23与32 | B. | m2n与$-\frac{1}{2}m{n^2}$ | C. | 2πR与π2R | D. | -x2y与2yx2 |
11.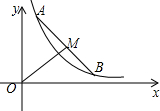 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
 如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )
如图所示是反比例函数y=$\frac{2}{x}$在第一象限内的图象,A,B为该图象上两个动点,且AB=4,若点M为线段AB的中点,则线段OM的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$-1 |
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
15.与$\sqrt{3}$+1最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
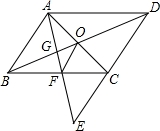 如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.
如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)