题目内容
5.计算(1)ym•ym+1
(2)20032
(3)1232-122×124.
分析 (1)根据同底数幂的乘法法则计算即可;
(2)由20032=(2000+3)2,再用完全平方公式计算可得;
(3)由1232-122×124=1232-(123-1)(123+1),用平方差公式展开、去括号、合并可得答案.
解答 解:(1)ym•ym+1=ym+m+1=y2m+1;
(2)20032=(2000+3)2
=20002+2×2000×3+32
=4012009;
(3)1232-122×124=1232-(123-1)(123+1)
=1232-(1232-1)
=1232-1232+1
=1.
点评 本题主要考查整式的运算、同底数幂的乘法、完全平方公式、平方差公式,熟练掌握整式乘法法则和乘法公式是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
14.计算(-2x+1)(-3x2)的结果为( )
| A. | 6x3+1 | B. | 6x3-3 | C. | 6x3-3x2 | D. | 6x3+3x2 |
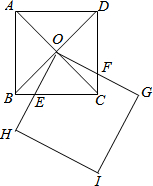 在边长为2的正方形ABCD中,对角线AC与BD相交于点O,另一个正方形OHIG绕点O旋转(如图),设OH与边BC交于点E(与点B、C不重合),OG与边CD交于点F.
在边长为2的正方形ABCD中,对角线AC与BD相交于点O,另一个正方形OHIG绕点O旋转(如图),设OH与边BC交于点E(与点B、C不重合),OG与边CD交于点F.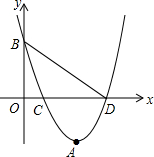 如图,已知抛物线的顶点为A(3,-3.2),且与y轴交于点B(0,4),交x轴于点C和点D.
如图,已知抛物线的顶点为A(3,-3.2),且与y轴交于点B(0,4),交x轴于点C和点D.