题目内容
15.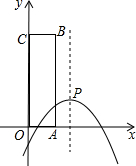 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.(1)点P的坐标为(2,m)(用含m的代数式表示);
(2)当点P在BC边上时,求对应的抛物线的函数关系式;
(3)点B是否会落在抛物线的下方,请说明理由;
(4)直接写出矩形OABC的各边与抛物线共有2个公共点时m的取值范围.
分析 (1)根据配方法,可得顶点坐标;
(2)根据P在BC上,可得关于m的方程,根据解方程,可得答案;
(3)根据自变量的值,可得相应的函数值;根据线段的和差,可得答案;
(4)根据图象与抛物线的交点大于一个小于三个时,可得不等式组,根据抛物线过点B、C,可得m点的在范围.
解答 解:(1)y=-$\frac{1}{2}{x}^{2}$+2x-2+m=-$\frac{1}{2}$(x-2)2+m,
顶点P的坐标为(2,m),
故答案为:(2,m);
(2)点P在BC边上时,yP=yC,m=6-m,解得m=3,
对应的抛物线的函数关系式y=-$\frac{1}{2}{x}^{2}$+2x+1;
(3)如图1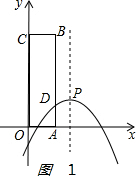 ,
,
设直线AB与抛物线的交点为D,
当x=m时,yD=-$\frac{1}{2}$m2+2m-2+m=-$\frac{1}{2}$m2+3m-2,
yB-yD=(6-m)-(-$\frac{1}{2}$m2+3m-2)=$\frac{1}{2}$m2-4m+8=$\frac{1}{2}$(m-4)2≥0,
点B不会落在抛物线的下方;
(4)
当点A在抛物线上时,如图2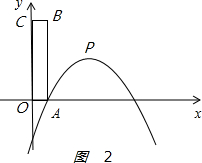 ,
,
-$\frac{1}{2}$m2+2m-2+m=0,解得m1=3-$\sqrt{5}$,m2=3+$\sqrt{5}$(不符合题意,舍),
当m=3-$\sqrt{5}$时,抛物线与矩形OABC的各边恰好有一个交点.
当点P落在BC上时,如图3 ,
,
m=3,抛物线与矩形OABC的各边恰好有三个交点.
当3-$\sqrt{5}$<m<3时,矩形OABC的各边与抛物线恰好有两个交点.
②当点B在抛物线上时,如图4 ,
,
yC-yB=0,6-m=-$\frac{1}{2}$m2+2m-2+m,
解得m=4,此时矩形OABC的各边与抛物线恰好有两个交点.
∵点C(0,6-m)在y轴的正半轴上,
∴当4≤m<6时,矩形OABC的各边与抛物线恰好有两个交点.
综上所述:矩形OABC的各边与抛物线共有2个公共点时m的取值范围是3-$\sqrt{5}$<m<3,4≤m<6.
点评 本题考查了二次函数综合题,利用配方法求函数顶点坐标;利用平行于x轴直线上点的纵坐标相等得出m的值是解题关键;利用图象与矩形交点的个数得出不等式是解题关键,要分类讨论,以防遗漏.

| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -5 | 1 | 3 | 1 | … |
①抛物线的顶点为(1,3); ②抛物线与y轴交于负半轴;
③抛物线开口向上; ④方程ax2+bx+c=0有两个不相等实数根.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
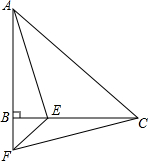 在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E,在BC上,BE=BF,连结AE,EF和CF,此时,若∠CAE=30°,那么∠EFC=30°.
在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E,在BC上,BE=BF,连结AE,EF和CF,此时,若∠CAE=30°,那么∠EFC=30°.