题目内容
7.化简:(x+1)(x2+1)(x4+1)…(x2048+1)(x-1)=x4096-1.分析 根据平方差公式计算即可得到答案.
解答 解:(x+1)(x2+1)(x4+1)…(x2048+1)(x-1)=(x+1)(x-1)(x2+1)(x4+1)…(x2048+1)=(x2-1)(x2+1)(x4+1)…(x2048+1)=(x4-1)(x4+1)…(x2048+1)=(x8-1)…(x2048+1)=x4096-1.
故答案为:x4096-1.
点评 本题考查了平方差公式,熟记平方差公式是解题的关键.

练习册系列答案
相关题目
18.下列方程,是一元二次方程的是( )
| A. | x2+3x-1=0 | B. | y2-5x=1 | C. | 2x+1=0 | D. | $\frac{1}{x}$+x2=1 |
19.已知实数a、b满足(a2-b2)2-2(a2-b2)=8,则a2-b2的值为( )
| A. | -2 | B. | 4 | C. | 4或-2 | D. | -4或2 |
17.下列变形中,不正确的是( )
| A. | 若x=y,则5+x=5+y | B. | 若-$\frac{x}{5}$=-$\frac{y}{5}$,则x=y | ||
| C. | 若mx=my,则x=y | D. | 若x=y,则2x-3=2y-3 |
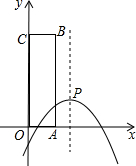 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.