题目内容
10.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -5 | 1 | 3 | 1 | … |
①抛物线的顶点为(1,3); ②抛物线与y轴交于负半轴;
③抛物线开口向上; ④方程ax2+bx+c=0有两个不相等实数根.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 结合图表可以得出当x=0或2时,y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3),借助(0,1)两点可求出二次函数解析式,从而得出抛物线的性质.
解答 解:∵由图表可以得出当x=0或2时,y=1,可以求出此函数的对称轴是x=1,顶点坐标为(1,3)①正确,
∴二次函数解析式为:y=a(x-1)2+3,
再将(0,1)点代入得:1=a(-1)2+3,
解得:a=-2,
∴y=-2(x-1)2+3,
∵当x=0时,y=1,
∴与y轴交点坐标为(0,1),故与y轴交于正半轴,②错误;
∵a<0
∴抛物线开口向下,故③错误;
∵y=-2(x-1)2+3=-2x2+4x+1,
△=16+4×2×1=22>0,
∴此方程有两个不相等的实数根,④正确.
正确的有2个.
故选:C.
点评 此题主要考查了二次函数的性质,二次函数解析式的求法,以及由解析式求函数与坐标轴的交点以及一元二次方程根的判别式的应用.

练习册系列答案
相关题目
11.下列各组线段,能组成三角形的是( )
| A. | 2cm 3cm 5cm | B. | 5cm 6cm 10cm | C. | 2cm 2cm 5cm | D. | 3cm 4cm 8cm |
18.下列方程,是一元二次方程的是( )
| A. | x2+3x-1=0 | B. | y2-5x=1 | C. | 2x+1=0 | D. | $\frac{1}{x}$+x2=1 |
5.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (-a2)3=a6 | C. | a3+a4=a7 | D. | a2•(a3)4=a14 |
19.已知实数a、b满足(a2-b2)2-2(a2-b2)=8,则a2-b2的值为( )
| A. | -2 | B. | 4 | C. | 4或-2 | D. | -4或2 |
20.在⊙O中,⊙O的半径为6cm,弦AB的长为6cm,则弦AB所对的圆周角是( )
| A. | 60°或120° | B. | 30°或150° | C. | 60° | D. | 30° |
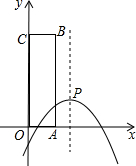 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.