题目内容
6.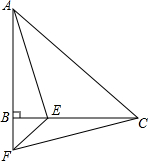 在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E,在BC上,BE=BF,连结AE,EF和CF,此时,若∠CAE=30°,那么∠EFC=30°.
在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E,在BC上,BE=BF,连结AE,EF和CF,此时,若∠CAE=30°,那么∠EFC=30°.
分析 根据已知利用SAS判定△ABE≌△CBF,由此可求得∠EAB=∠FCB,根据已知利用角之间的关系可求得∠EFC的度数.
解答 解:在△ABE和△CBF中,
∵$\left\{\begin{array}{l}{BE=BF}\\{∠ABC=∠CBF}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△CBF(SAS),
∵AB=BC,∠ABC=90°,∠CAE=30°,
∴∠CAB=∠ACB=$\frac{1}{2}$(180°-90°)=45°,∠EAB=45°-30°=15°.
∵△ABE≌△CBF,
∴∠EAB=∠FCB=15°.
∵BE=BF,∠EBF=90°,
∴∠BFE=∠FEB=45°.
∴∠EFC=180°-90°-15°-45°=30°,
故答案为:30°.
点评 此题主要考查了全等三角形的判定方法及等腰三角形的性质等知识点的掌握情况,本题的关键是能证得△ABE≌△CBF,证出∠EAB=∠FCB.

练习册系列答案
相关题目
18.下列方程,是一元二次方程的是( )
| A. | x2+3x-1=0 | B. | y2-5x=1 | C. | 2x+1=0 | D. | $\frac{1}{x}$+x2=1 |
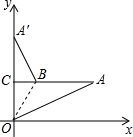 如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.
如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.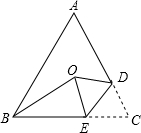 如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.
如图,在等腰△ABC中,AB=AC,将△ABC沿DE折叠,使底角顶点C落在三角形三边的垂直平分线的交点O处,若BE=BO,则∠ABC=63度.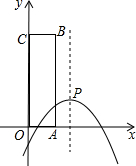 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x}^{2}$+2x-2+m的顶点为P,点A(m,0)在x轴正半轴上,点C(0,6-m)在y轴正半轴上,以OA、OC为边作矩形OABC.