题目内容
2. 如图,在矩形ABCD中,AB=8,AD=12,过点A,D两点的⊙O与BC边相切于点E,求⊙O的半径.
如图,在矩形ABCD中,AB=8,AD=12,过点A,D两点的⊙O与BC边相切于点E,求⊙O的半径.
分析 首先连接OE,并反向延长交AD于点F,连接OA,由在矩形ABCD中,过A,D两点的⊙O与BC边相切于点E,易得四边形CDFE是矩形,由垂径定理可求得AF的长,然后设⊙O的半径为x,则OE=EF-OE=8-x,利用勾股定理即可得:(8-x)2+36=x2,继而求得答案.
解答 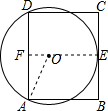 解:连接OE,并反向延长交AD于点F,连接OA,
解:连接OE,并反向延长交AD于点F,连接OA,
∵BC是切线,
∴OE⊥BC,
∴∠OEC=90°,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDFE是矩形,
∴EF=CD=AB=8,OF⊥AD,
∴AF=$\frac{1}{2}$AD=$\frac{1}{2}$×12=6,
设⊙O的半径为x,则OE=EF-OE=8-x,
在Rt△OAF中,OF2+AF2=OA2,
则(8-x)2+36=x2,
解得:x=6.25,
∴⊙O的半径为:6.25.
点评 此题考查了切线的性质、垂径定理、矩形的性质以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
12.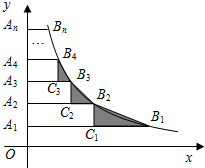 如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )
如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )
 如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )
如图,在y轴正半轴上依次截取OA1=A1A2=A2A3=…=An-1An(n为正整数),过A1,A2,A3,…,An分别作x轴的平行线,与反比例函数y=$\frac{2}{x}$(x>0)交于点B1,B2,B3,…,Bn,如图所示的Rt△B1C1B2,Rt△B2C2B3,Rt△B3C3B4,…,Rt△Bn-1Cn-1Bn面积分别记为S1,S2,S3,…,Sn-1,则S1+S2+S3+…+Sn-1=( )| A. | 1 | B. | 2 | C. | 1-$\frac{1}{n}$ | D. | 2-$\frac{1}{n}$ |
10.如图由圆形组成的四个图形中,可以看做是中心对称图形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
7. 如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )
如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )
 如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )
如图,在⊙O中,弦AB、CD相交于P,若∠A=30°,∠APD=60°,则∠B等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
14.下列命题中,正确的是( )
| A. | 三角形的一个外角大任何一个内角 | |
| B. | 等腰三角形的两个角相等 | |
| C. | 三个角分别对应相等的两个三角形全等 | |
| D. | 三角形的三条高可能在三角形内部 |
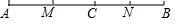 (1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,M,N分别是AC,BC的中点,求线段MN的长度.