题目内容
13.解方程(1)9(x-2)2=4(x+1)2
(2)$\sqrt{3}{x^2}-x=2\sqrt{3}$.
分析 (1)利用直接开平方法解方程即可;
(2)先移项,使方程的右边化为零,再将方程左边分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
解答 解:(1)9(x-2)2=4(x+1)2,
[3(x-2)]2=[2(x+1)]2,
直接开平方,得
3(x-2)=2(x+1),或3(x-2)=-2(x+1),
解得,x1=8,x2=$\frac{4}{5}$;
(2)$\sqrt{3}{x^2}-x=2\sqrt{3}$,
移项得,$\sqrt{3}$x2-x-2$\sqrt{3}$=0,
分解因式得,(x-$\sqrt{3}$)($\sqrt{3}$x+2)=0,
x-$\sqrt{3}$=0,或$\sqrt{3}$x+2=0,
解得,x1=$\sqrt{3}$,x2=-$\frac{2\sqrt{3}}{3}$.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
4.已知代数式-5am-1b6与$\frac{1}{2}a{b^n}$是同类项,那么m-n的值是( )
| A. | 5 | B. | -5 | C. | 4 | D. | -4 |
8.下列事件中为必然事件的是( )
| A. | 从一定高度落下的图钉落地后顶尖朝上 | |
| B. | 打开数学课本时刚好翻到第60页 | |
| C. | 早晨太阳一定从东方升起 | |
| D. | 今年14岁的小明一定是初中学生 |
18. 如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )
如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )
 如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )
如图,图中数字表示所在正方形的面积,则字母B所代表的正方形的面积是( )| A. | 196 | B. | 144 | C. | 13 | D. | 12 |
 Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AC于E,若BC=8,DE=3,则CD的长度是5.
Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AC于E,若BC=8,DE=3,则CD的长度是5. 如图所示:已知O为AB上一点,∠BOC=46°,OD平分∠AOC,∠AOD=67°.
如图所示:已知O为AB上一点,∠BOC=46°,OD平分∠AOC,∠AOD=67°.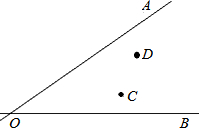 如图所示,成纪大道与天北高速在七里墩相交于点O,在∠AOB的内部有工厂C和D,现要建一个货场P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹)
如图所示,成纪大道与天北高速在七里墩相交于点O,在∠AOB的内部有工厂C和D,现要建一个货场P,使P到OA和OB的距离相等,且使PC=PD,用尺规作出P点的位置.(不写作法,保留作图痕迹) 如图,在矩形ABCD中,AB=8,AD=12,过点A,D两点的⊙O与BC边相切于点E,求⊙O的半径.
如图,在矩形ABCD中,AB=8,AD=12,过点A,D两点的⊙O与BC边相切于点E,求⊙O的半径.