题目内容
设函数y=
与y=x-2的图象的交点坐标为(a,b),则
+
的值为 .
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
考点:反比例函数与一次函数的交点问题
专题:
分析:据反比例函数与一次函数的交点问题,解方程组
可得到交点坐标,则得到a与b的值,然后把a、b的值代入
+
中计算即可.
|
| 1 |
| a |
| 1 |
| b |
解答:解:根据题意得
,
解得
或
,
所以函数y=
与y=x-2的图象的交点坐标为(1+
,
-1)或(1-
,-
-1),即a=1±
,b=-1±
,
所以
+
=
+
=2
+
=
+
=-2
故答案为2
或-2
.
|
解得
|
|
所以函数y=
| 1 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
所以
| 1 |
| a |
| 1 |
| b |
| 1 | ||
|
| 1 | ||
|
| 2 |
| 1 |
| a |
| 1 |
| b |
| 1 | ||
-
|
| 1 | ||
-
|
| 2 |
故答案为2
| 2 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
相关题目
 如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.
如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.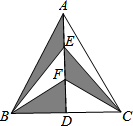 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是 四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?
四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?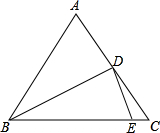 如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD交BC于点E,求证:CD=
如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD交BC于点E,求证:CD= 如图,在B港有“远望1号”和“远望2号”两艘轮船同时出发,若“远望1号”轮船沿北偏东60°方向每小时行驶8n mile,“远望2号”轮船沿南偏东30°方向每小时行驶15n mile,两小时后,两艘轮船分别到达M岛和N岛,求M岛和N岛之间的距离.
如图,在B港有“远望1号”和“远望2号”两艘轮船同时出发,若“远望1号”轮船沿北偏东60°方向每小时行驶8n mile,“远望2号”轮船沿南偏东30°方向每小时行驶15n mile,两小时后,两艘轮船分别到达M岛和N岛,求M岛和N岛之间的距离.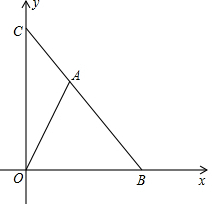 如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合.
如图,已知点B的坐标为(4,0)点C的坐标为(0,4)点A在线段BC上,且不与点B,C重合.